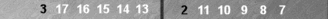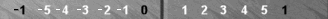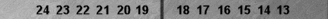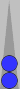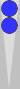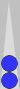Welcome to the renovated series of Naccel 2 posts. The diagrams are Naccel
numbered, which by itself is a big improvement. Further, as a
consequence, I have been able to improve the textual explanations as
well.
This renovation would not have been possible without Matt Ryder's enthusiasm
and html expertise. Before reading on, you might want to take a minute
to check out Matt's Naccel diagram FAQ.
This Naccel 2 post #1 is in response to Lucky Jim's post, under an old "Kangaroo Count" thread and repeated below.
|
I have come across a pip-counting approach which Nack wrote about sometime ago—this looks very interesting to me. Click here: aN ACCELerated Pipcount.
I wonder if Nack could let me know if he still uses this approach and if he would still advocate it?
|
Yes, I certainly do advocate it. I counted fastest when I was using Naccel.
Many
years ago, I started experimenting with other pipcount systems (over
thirty), counting pips various ways to relieve boredom while waiting
for my opponents to move. (Hopefully clocks will put this problem
behind us soon.) I skip around with counting systems now, as the mood
strikes me.
I can explain Naccel much more simply than I did in my article that appeared in the quarterly magazine Backgammon Today
(Sep., 2001). Indeed the approach is so modernized that I've adopted a
suggestion made a few months ago (I forgot by whom) to call it "Naccel
2."
There
are four Super-points, or "Supers," in Naccel, numbered 0, 1, 2 and 3
in black below, which also double as the Naccel 0pt, 6pt, 12pt and
18pt, as you will be able to deduce if you examine the sequence of
white Naccel point-numbers labeling the diagrams.
If
you are familiar with the traditional numbering system, you will also
recognize the four Supers as the traditional 6pt, 12pt, 18pt and 24pt,
respectively. Naccel point numbers are 6 smaller than
traditional point numbers all the way around the board, as illustrated.
Hereafter, I will shorten the word "traditional" to "trad."
In the diagram below, I've placed a Blue checker on each of the Supers.
     
 
     
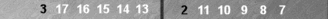
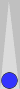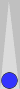
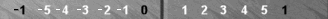
The four Super-points
For
counting purposes, you can, and should, ignore the checkers on the 0pt
(trad 6pt). They count zero. The other three Supers can be counted just
like the lower three points in a bearoff.
To get a feel for how easy it is, I've changed the point-numbering to trad(itional) just for this one diagram:
 
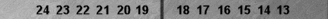
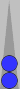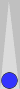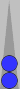
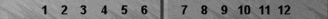
Simple traditional bearoff
Using
trad pipcount, I'll bet you can count this bearoff position quickly.
There are two checkers on the 1-point (=2), one on the 2-point (=2), and
two on the 3-point (=6), for a total of 10 pips.
This
same trivial method used to count the 1-, 2- and 3-points in trad can
be used to count the 1-, 2- and 3- Supers (Super-points) in Naccel.
This is illustrated in the diagram below.
 
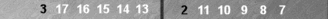
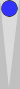
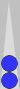
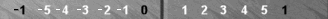
Count as you did before
And
here we are. There are two checkers on Super1 (=2), one on Super2 (=2),
and two on Super3 (=6), for a total of 10 super-pips, or more commonly
"10 supes," or sometimes "10s" (pronounced "ten es"), or simply "10."
Note
that you ignore the checkers on Super0 (trad 6pt) in exactly the same
way you ignored the checkers in the bear-off tray in the previous
diagram.
If
you're not sure how the count of 10 was arrived at, or how the counting
is similar to the traditional bearoff count of 10 pips in the previous
diagram, please review.
Now
that you know where the Supers are and how they are counted, I'll begin
to demonstrate the joys of the focal point that you have until now
known only as the 6pt (six-point). This is the center of the Naccel
universe, and it is both Super0, or "S0," and the Naccel 0pt, or "n0." If you take up Naccel, you'll never have to count the checkers on the trad 6pt (or "t6") again.
Let's have a look at that beautiful beast, in context.
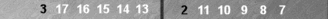
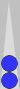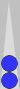
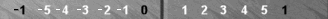
Count of zero
This is a common near-side formation that arises after an opening 42 is played. The stack of four checkers on the Naccel 0pt, n0 (trad 6pt, t6), count zero—they are invisible (or soon will be to your trained eye).
The
two-checker point on the left (trad 4pt, but −2pt in Naccel) and the
two-checker point on the right (trad 8pt, but the 2pt in Naccel) are
equidistant from the (0-count) stack in the middle. They cancel each
other out, thereby also yielding a count of zero. When you get used to
seeing this formation (and many others like it), it will, in its
entirety, vanish into thin air.
Now let's be bold and tackle a full fifteen checker position:
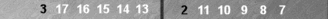
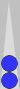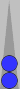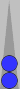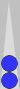
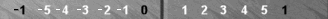
Near side goes POOF
Here,
the four checkers on the 0pt are invisible, and ... you guessed it: by
cancellation, the four points reflected around the 0pt are also invisible. The entire near side goes POOF!
All
that needs to be counted in this position are the three checkers on the
far side of the board. The two checkers on S2 (Super2) count 2 × 2 = 4,
and the one checker on S3 counts 3, for a total of 7. That is Blue's entire count.
"But 7 doesn't mean anything to me."
It
does when you compare it to your opponent's similarly small count (and
if you want to apply a race formula, Naccel has one). But we're getting
ahead of ourselves. For now, do it the "hard" way: multiply by 6 and
add 90—which in this case comes to 132.
That's
enough for now. If this subject sparks enough reader interest, I'll
follow up with post #2. Perhaps
it would be most effective if someone interested in Naccel sends me a
full board position (one s/he found difficult to count, or not,
whatever), and I'll develop my explanations around that. In this way,
readers can get a glimpse of the lightning counts they can ultimately
achieve should they want to pursue Naccel 2 further.
Go on to Part 2.
|
