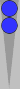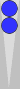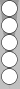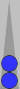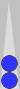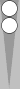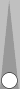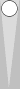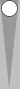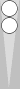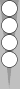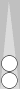|
This is Part 6 of the Naccel 2 series.
The basic squads you have learned thus far are the six-stack, triplet, and pair. There are also shift-variants of these squads, some of which you've seen (various six-syms and the wedge), but we'll put those aside for now.
Today,
we'll look at another basic squad called the "block." Whereas the
others mentioned above use six, three or two checkers, this squad uses
four:
The block just to the right of the Naccel 0pt (trad 6pt) arises after Blue plays a standard opening 61.
To count a block—or indeed any two points on the board—add together the point numbers and divide by 3. The near-side block occupies the (Naccel) 1pt and 2pt, so: 1 + 2 = 3, divided by 3, gives you a count of 1.
The
block on the other side of the board, formed by the four back checkers,
is on the 16pt and 17pt. Summing these point numbers gives you 33, and
dividing by 3 gives you 11. (By the way, blocks always generate odd-numbered
counts.)
[An
alternate counting method for blocks: Count three checkers as being on
the nearest Super and the other as being on the second nearest Super.
So, here, the near block counts (0 × 3) + 1 = 1, and the far block
counts (3 × 3) + 2 = 11.]
As
always, the 0pt checkers are invisible. Blue's entire position counts
11 + 1 for the blocks, plus 2(2) for the mid, for a total of 14(2).
Next, let's have a look at some useful ways to combine two checkers on the midpoint with a near side point:
You recognize this formation as a mirror.
The number of total checkers in a mirror gives you the count, so this mirror counts 4.
To
reach the next formation, we will "zig" (move forward) the near-side
point 3 pips. Two checkers times 3 pips is a total of 6 pips, or one
supe, which means the overall count of 4 is reduced below by 1, to 3:
This formation is called a "zig mirror" or "zig" for short. A zig
counts 3, one less than a regular mirror. [Zig is both a noun that is
short for zig mirror, and a verb that means to move a point 3 pips
forward.] For reference, if you drop the far-side point of a zig mirror
straight down, the near-side point always leads it by 4 pips.
You
can also count a zig in the same way you count a block (or any two
points): add the point numbers and divide by 3. So, here (7 + 2) ÷ 3 = 3.
This
zig is a combination of a stripped midpoint and stripped 2pt (trad
8pt). Also, as early as the opening roll, a "double zig" occurs when an
opening 5 is brought down, creating a stack of four checkers on each
point; the entire right side then counts 6.
Note
that if you hop the two midpoint checkers down to the (Naccel) 1pt, you end up with the near-side block in the first diagram of this post.
That block counts 1, and adding the 2 hops
imagined here is another way to achieve the count of 3 for the diagram directly above.
This hop example, and the series of zigs we're performing, help illustrate
that all Naccel formations can be built and rebuilt upon board
symmetries and simple, logical techniques.
Let's zig the front point again, thereby further reducing the count by 1:
This position is called a "diagonal mirror," or "diag" for short.
To count a diag, divide the number of checkers in the formation by 2. Here there are four checkers, so the diag is 2. This is 1 less than a zig (previous diagram) or 2 less than a point mirror (two diagrams back).
An easy way to reconcile this count of 2 is to hop the two midpoint
checkers (+2) to the bar point, creating a little poof. Another way is
to shift the midpoint to S1 (count of 2) and the −1pt to S0 (count of 0).
As your pattern recognition improves, you will spot (or create) larger groups that are combined from smaller ones. For example ...
The left-hand diagram is a combination of the previous two diagrams. Two "mids" (midpoint checkers) plus the −1pt are a diag (+2), and two mids plus the 2pt are a zig (+3). If you see this formation enough times, the eight checkers (plus any that are on S0) will jump out as an instant +5.
The right-hand diagram puts the formation in a context. Blue's entire position counts +5 (midpoint and near side) + 7 (triplet) = 12.
Continuing from the Diag diagram, letís zig
the front point forward one last time:
The previous formation counts 2, so this one counts 1. If you like, you can
call this formation a diagonal "zig mirror," or "dizig" for short. However,
the only other formation with the same relationship, one space to the
left, rarely arises; so rather than fill your head with the term "dizig," it
might be easier just to remember this specific midpoint formation as 1.
Okay, now let's add a specially selected pair to the above formation.
And here it is. Midpoint plus −4pt counts +1, and the pair on the −3pt
counts −1. This important six-checker formation counts zero: I call it
a midpoint poof or "midpoof" for short.
If you shift the two low points outwards, so that Blue instead owns the
−5pt (trad 1pt) and −2pt (trad 4pt), that is also a midpoof, though it
arises less frequently in practice.
Commit the diagrammed midpoof to memory, and you will encounter it often in
your Naccel adventures. We'll even have a chance to use the midpoof
later in this post.
Now we'll look at midpoint formations on the far side of the board.
This far-side reflection counts the same as if you were to stack all four checkers on S2 (the
point around which they reflect).
In other words, double the numbers of checkers you see: that gives you a count of 8.
Okay, let's zig (move forward) the back point, reducing the count by 1:
I call this formation "midgold" because it combines the midpoint with
the golden anchor. It counts 1 less than the far-side reflection of 8,
which makes it 7.
There are many other ways to reconcile midgold as a count of 7. To name a
few:
- Add the point numbers 14 + 7 and divide by 3.
- Shift the anchor back a point to get a 5-count pair and the midpoint forward to S1 (count of 2);
- Shift one midpoint checker forward 7 pips to the 0pt and the other back 7 pips to the anchor, creating a 7-count triplet there.
Midgold occurs with regularity, so you would do well to remember that its count is 7.
We'll even have a chance to apply midgold later in this post.
Let's zig the back checkers forward again, but we'll skip over the next spot
because Opponent typically occupies her 2pt (trad 8pt). Instead we'll zig
twice, reducing the count from 7 to 5. Can you visualize the resulting
formation, and what is another way to count it (other than 7 − 2)?
Answer below.
Having hopped (or zigged twice) from the gold part of midgold, you now have
a block.
I call this block "midblock," because it contains the midpoint. To count
it, sum its point numbers 8 + 7 and divide by 3, for a count of 5.
When you have four (or more) checkers on the midpoint and you need a back 2-pip countershift, the midblock is very handy.
Let's look at Lucky Jim's most recent submission:
First, let's count Blue.
Maik
quickly spotted Blue's near-side poof: simply move the 2pt spare back,
covering the 3pt, and lift the 1pt blot to the 0pt. Poof!
(If you don't see the poof, please review the last two diagrams of Part 1, the last diagram of Part 2 (especially), the second diagram of Part 4, and the fourth diagram of Part 5.)
There's nothing on the near side to "count."
That leaves the far side. Aha, midgold = 7; that's Blue's entire count!
Let's repeat the diagram with point numbering from White's perspective:
For the White count, I recommend this simple 1-pip shift:
Do you see the midpoof?
It is the six-checker formation composed of the
midpoint and the four low-point checkers: count of zero. And of course
the (invisible) 0pt checkers also count zero.
You need count only the six checkers on the top right. This is simply a
six-stack on the (Naccel) 2pt plus 1 pip.
White's entire count is 2(1).
Go on to Part 7, or read more below.
| 




![]()