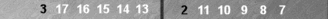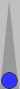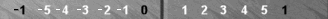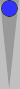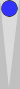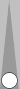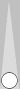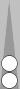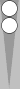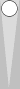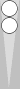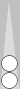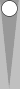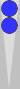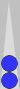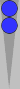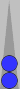|
This is Part 11 of the Naccel 2 series. In this post, I will
- Advance your understanding of midblot counts.
- Reinforce some earlier material.
- Illustrate a new formation.
- Count full board positions (as usual).
To review midblot counting, read this section of Part 8.
An example of a common midblot count is shown below:
Here, the blot is located on the third point in front of the Super,
which combines well with the three checkers on the midpoint. To count,
you add this 3 to the Super, which in this case is S1, for a count of
4.
In Part 8, I introduced this formation as "midblot three/third + S1," and
I later abbreviated it to "midblot 3 + S1." I'll now abbreviate it
further to "m3+1" and henceforth that will be the main way that I write
it.
Let's review what that formation looks like when we move the blot to the back quadrant:
This formation is midblot three/third + S3, or midblot 3 + S3, or
simply m3+3. Just add 3 + 3 to get a count of 6. (Note that you can
double-hop the blot to reach the previous position, which has a count
of 4.)
With a slightly more advanced application of midblot counting, you can often combine the midpoint with two or more checkers. For example:
Here, the blots are 1 + 2 = 3 pips ahead of the Super, and can
therefore be combined with three checkers on the midpoint (just as
surely as one blot 3 pips ahead of the Super can). You simply add S3 twice instead of once to get the proper count.
The
formation above is m3+3+3 = 9. The first 3 refers to number of pips in
front of the Super and the matching number of checkers on the midpoint,
and the other two 3's represent S3 for each checker in that quadrant.
Longhand, this might be written "midblot three + S3 + S3 = 9."
[Note
that you can break the above formation into two midblots, m1+3 and
m2+3, allocating one midpoint checker to the backmost blot and two
midpoint checkers to the other blot. But once you grasp the concept of
combining, m3+3+3 is faster.]
Below is a similar but larger example, and to mix things up I'll switch colors:
The blots are a total of 5 pips in front of the Super, which match up well with the five checkers on the midpoint. And S3 gets added twice, yielding
m5+3+3 = 11.
If the two "blots" happen to be on the same point, it works the same way:
In the left-hand diagram, the back checkers are a total of 4 pips in front of the Super, which match up with the four checkers on the midpoint. Add S3 twice, yielding
m4+3+3 = 10.
If you hop the two back checkers forward, reducing the count by 2, you
get the formation in the right-hand diagram, which counts
m4+2+2 = 8.
Hop the anchor forward again, and you get
In the left-hand diagram, the near side checkers are a total of 4 pips in front of the Super, which match up with the four checkers on the midpoint. Add S1 twice, yielding
m4+1+1 = 6.
If you hop the point forward yet again, you reach the right-hand diagram, which is counted as
m4+0+0 = 4.
It's really quite simple, once you get the hang of it.
You can even combine the midpoint with checkers in different quadrants. For example:
The anchor is 2 + 2 = 4 pips in front of its Super, and the blot is 1
pip in front of its Super, and the for a total of 5 pips. That 5 pips
matches up with the five checkers on the midpoint. The formation is counted as
m5+3+3+0 = 11.
It might take a while to build up to such counts, but in the meantime you can break this down into two formations:
m4+3+3 = 10;
m1+0 = 1.
The
first line is for the anchor: 4 pips / four midpointers, S3+3. The
second line is for the blot: 1 pip / one midpointer, S0 (also known as
a blot diag).
Let's revert to a simpler example:
If you like, you can count this formation as m2+0+0 = 2. However, you
already recognize this as a diagonal mirror or diag that counts 2.
If
you hop the n−1 point backwards (to n5), you increase the count by 2,
to 4, and get a regular mirror. If you hop the point backwards again, you increase the count by another 2, to 6, and it looks like this:
If you like, you can count this as (a midblot) m2+2+2 = 6, or you can see it as a double wide squad: (n11 + n7) ÷ 3 = 6. Or if you know midgold = 7 and midblock = 5,
you can see this formation is exactly in between and therefore a count
of 6. Regardless of how you count it, sooner or later, you'll know it
as an instant 6, as I do.
From this formation, if you shift the points outward by a pip, the count remains at 6 and the new formation looks like this:
The
formation in the left-hand diagram is called a reverse diagonal mirror,
or rev diag, or simply "rev." A (point) rev counts 6.
For
reference, a "blot rev" (one checker on each point) is shown in the
right-hand diagram. A blot rev counts 3 (half of a point rev).
Basically, the count of any rev is half again the number of checkers in
the formation.
Let's switch colors (from White to Blue) and slide the points to the left a few pips:
Like mirrors and diags, opposing checkers of revs are on the same color.
Another
important clue for any mirror-type formation (mirror, zig, zag, diag,
rev, ...) is that opposing checkers are either already on Supers or pair
points, or they can be equally shifted to get there.
In
the left-hand diagram, for example, a 1-pip shift and countershift to
the right transforms both points into pairs, as shown in the right-hand
diagram: pair 5 + pair 1 = rev 6.
Alternatively,
the points in the left-hand diagram can be equally shifted 2 pips to
the left, which gives you two checkers on S3 plus two (invisible)
checkers on S0, again for a count of 6.
The
revs in the above left-hand diagram and previous left-hand diagram will
soon be used in our full-board counting; so, you might want to quickly
review them now.
The midpoint is a useful collector of "leftover counts" (see Part 10).
For example, three checkers on the midpoint are 3(3). There are times,
though that you can combine a would-be integer count with a leftover
count and save a step. For example ...
You can count these six checkers as a triplet 1 plus a leftover midpoint count of 3(3), for a total of 4(3).
Alternatively,
you can count this formation as a tweensym (written as one word or
two). These six checkers are grouped symmetrically around the imaginary 4½ point; the count is therefore 4(3).
Here is a related example:
You can count 1 for the triplet, and 1(3) for the off-triplet (i.e., divide n3 by 2), for a total of 2(3).
It is faster, though, to count this as a tweensym. Six checkers around the (imaginary) 2½ point count 2(3).
On to full board counting.
Our first position is supplied by Ian (in this post) and shown in the left-hand diagram below. We will start by looking just at Blue:
Ian also provided the right-hand diagram above, in order to demonstrate a
3-pip shift/countershift that leads to a fast count for Blue using the
Cluster Count system. I've also pasted his cluster count below:
30 for the six point stack
10 for the five point pair
30 for the stack shifted onto the 10 point
40 for the pairs on the midpoint+barpoint
+7 for the left over on the barpoint
Total 117 (it's easy to keep a running count on your head when it's all in 10s.)
|
"Can Naccel count this faster?"
Here is how I would respond (using the original position in the left-hand diagram):
The same Naccel count can be applied to the shifted (right-hand) position, but of course, it's easier to count without
shifting (left-hand) when you have the choice. In short, for this
position, Naccel uses two subcounts compared to Cluster's five
subcounts, plus there is no pre-shift.
Isolating
the six checkers in the lower right (of the left-hand diagram), Lucky
Jim counted the triplet as 1, and the odd-point three-stack as 1(3);
that's a good way to do it if you don't know/remember the tweensym
technique. (In fact, if your leftover counting is less sophisticated
still, you can break down that six-checker portion to triplet 1 + pair
1 + n3 blot = 2(3).)
Here is Ian's full board position with both colors:
Now we'll repeat the position just for White but with (two types of) motion:
The right-hand diagram represents Ian's 2-pip shift (2 pips) in each direction. His Cluster Count is:
50 for the 24+midpoint combination,
50 for opposing pairs on both six-points (leaving two over on White's six point),
30 for the block on the 7 and 8 points,
leaving +12 and +6 for the four remaining inner-board chequers.
Total 148.
|
The left-hand diagram also shows 2 + 2 = 4 pips of motion, except it is all
in the same direction (forward). With the pair/block poof (ten checkers) around S0 poofed, the Naccel count is:
S3,
rev 6,
plus 4p motion.
Total = 9(4).
|
For reference, White trails Blue by 9(4) − 4(3) = 5(1).
Jim
and Petter counted much the same way, using 2 pips of motion to poof
White's near side, and the other 2 pips to create the rev. The only
real difference is that they didn't actually know the formation as a rev (prior to this post), so they counted the Supers piecemeal as S2+2 + S1+1 = 6.
As an alternative, you can just as easily move White's other
far-side point forward, as shown below. White's double wide in the
lower right counts 6.
The second position, diagrammed below, is brought to us by Petter. (He credits the origin in his post.)
For Blue, the count is m3+3+3, plus triplet 1 plus a pip = 10(1).
Can
you follow that? You can review the five-checker formation on the far
side (m3+3+3) earlier in this post, but basically, the back checkers
are 3 pips in front of the Super, which match the three
checkers on the midpoint, and you add another 3 for each of the blots
near S3. Ian and Jim came up with the same correct 9 count portion by
shifting to the Supers: S3+3 + S1+1+1 = 9.
The
small poof consisting of the seven n−1, n0 and n1 checkers we all
simply ignored. That leaves two checkers on n2 and one on n3. If the n3
checker is moved forward a pip, a triplet of 1 is formed; hence the
leftover count is 1(1).
Petter's
count is interesting: he shifted the back checkers to S3 and the two n2
checkers to S0 (nine-checker poof), for a net motion of +1 pip. The
four checkers remaining on the right are m3+1, plus S3+3 comes to 10,
plus the 1p motion makes 10(1).
I'll
describe a faster variant of that: Simply move the backmost checker 1
pip forward, as shown below, left. This creates a rev composed of the
n16 and n2 points, for a count of 6 (while the seven checkers to the
left of n2 still poof). For the four rightmost checkers add m3+1 in the
same way, plus the initial 1p motion, yields a count of 10(1).
To further clarify visually, I've removed the small (seven-checker) poof in the right-hand diagram, leaving just the rev and the m3+1 formation.
Let's repeat the position with White numbering:
You
can, of course, count this as an opening position of 12(5) minus 5 pips
moved = 12. If you know a reference position, you may as well use it.
But for practice, let's pretend we're not that lucky.
I count White as m5+3+3+0 plus triplet 1 = 12.
White's anchor and blot, together, are 5 pips in
front of the Supers—matching to the five checkers on the
midpoint—and the checkers are near S3, S3 and S0. Hence the count is
m5+3+3+0, and the triplet adds 1 more, for a total of 12.
If
you can't quite wrap your mind around that midblot count, you can break
it into two pieces, both of which are diagrammed or implied earlier in
this post: (a) m4+3+3, and (b) m1+0. (Plus the triplet 1 gives a total
of 12.) The m4+3+3 formation involves four midpointers plus the two
back checkers (4 pips in front of S3). The m1+0 is just a blot diag
(one midpointer plus the n−1 blot).
An
alternative midblot method that you might find easier is to shift
forward one of White's back checkers 1 pip, and countershift her n−1
checker to n0 (making it disappear), as shown in the right-hand diagram. This gives you m5+3+3 + triplet 1 = 12.
Once
you become comfortable with midblot counting (a matter of practice),
more formations will become instant counts to you, and you'll be closer
to performing lightning counts for a wide variety of positions.
Petter
found a pleasing White count: shift the blot 8 pips back to her
midpoint and (equally) countershift the anchor 4 pips to S2. That
yields a count of S2+2 + midstack 7 + triplet 1 = 12.
Jim
hopped a midpointer to n1, poofing with n−1. Then he shifted the other
four midpointers to S1 and the back checkers to S3. That yields S3 + 3 +
S1 × 4 + triplet 1 + motion 1 = 12.
Ian
shifted the anchor forward and the midpointers all 1 pip forward, and
the n−1 checker back 1 pip (that's +2 + 5 − 1 = net +6 pips motion). He
counted pair 5 + S1 × 5 + triplet 1 + motion 1 = 12.
Again,
all this shifting to Supers works well enough, but if you put a bit of
effort into learning the midblot logic, your counts will become even
faster.
Go on to Part 12.
| 


![]()