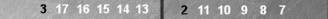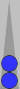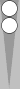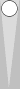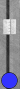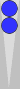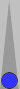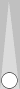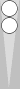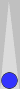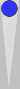We will walk through Jim's count of a position in detail. I hope he can forgive any critique that seems less constructive than it is fully intended to be. We can all use help in improving our counting habits.

For this post, I felt that including diagrams other than the main position would interrupt the flow. While not essential, it might help to set up the position below and follow along on a board.

For reference, a faster count for Blue in this position is illustrated in this diagram above.

Counting Habits

In the interest of being efficient, for the most part, I'll be sticking to the general Naccel posts rather than addressing individual counts. Today, I'm going to make an exception because I have noticed some counting pitfalls worth discussing.

Your notes start below the position diagram, in italics.

	4(1)

With this position the approach I took was as follows: Blue: For counting purposes the man on the bar needs to go on the 24 point so that is one pip forward to the 24 point for a count of 3(1).

A poor start. Leading off with a fractional count slows down the count and reduces your options. Not only do you have to carry a separate baby pip-count around, but you can no longer use the roofer as a shifter or as an offset checker (in case that comes in handy)—he's gone. Maybe you'll get lucky and snag integer counts the rest of the way, but the best you'll do is break even.

If you must lead off with a single checker, make it part of an integer formation or at least hop it (i.e., 6 or a multiple of 6 pips) onto another blot or to an existing point to consolidate the board position (minimize confusion).

The midpoint is often a good place to hop a roofer (a movement of +2) because I have created special formations involving the midpoint and it is a great collector of leftover counts. (It's easy to multiply 1(1) by the number of checkers there.)

In the actual position, the midpoint is vacant, but the bar point (Naccel 1pt) turns out to be a magnificent landing spot. You can wipe out twelve checkers with a single blow (and any integer count it happened to be would be fine—the fact that the −3 count and +3 hop exactly offset is a further bonus). You could then finish with a dual purpose 4-pip shift: back up the far-side point to S2 (= 2 × 2), and slide the lower right blot forward to the 1pt, for a count of 4(1).

Oh, one more thing. Please refer to points by Naccel numbering (trad minus 6), which is intimately connected to the counts of the formations: get in the habit immediately. For example, the highest point on the board is "S3" or the "18pt," or you can say "Naccel 18pt" or "n18" as an occasional reminder). If you want to reference trad for some reason, "trad 24pt" or "t24" works.

For the remainder of this post, I will convert your point numbers from trad to Naccel. The square brackets designate my edit of your original text.

I moved the man on the blue [(Naccel) 1pt] 4 pips backwards to go on top of the checker on the [5pt] so as to create a zag for 5(−4).

Okay, you didn't know/see the six-prime, but the zag is a nice consolation prize (and shows you've paid attention). However, instead of carrying around another 4 pips in baggage, you should be looking for a way to countershift 4 pips profitably (or at least neutrally). The only place left is in the inner board, so that's where you do the deed.

Probably the best 4-pip countershift is lifting the −1pt checkers to the −3pt. That separates the irrelevant 0pt from the rest of the pack so it is easy to see what you have left, and, more importantly, it creates a pair (−1) atop a three-prime (−3). Indeed, that would complete the count.

This means we are running with a net (−3 pips).

Right (if you are referring solely to the baby pips and not the supes also accumulated thus far): the +1 pip from the 3(1) leadoff, and the −4 pips from the one-sided shift to the zag. The questionable technique of counting the 4 pips instead of countershifting aside, note there was no advantage in leading off with the roofer. Even if you find no way to use it, counting the extra pip last (or at least as late as possible) is simpler.

The six-sym around n−3 gives a count of −3.

Okay, good, that's the best you have now. However (if you can pardon me driving the point home) note that if you still had the roofer, you could either: (a) hop it +3 to the (now vacant) bar point and wipe out the −3 three-prime so that you don't have to alter your running supe count; or (b) cancel the +3 against the −3 and alter your count by only the leftover pip. Of these two choices, (a) is usually better technique, and in a moment you'll see the benefit.

There are two pips to move back from the n−1 point to the n0 point so add those to the existing −3 pips gives a total of −5 pips.

If you had still had the roofer and chose method (a) above, you could cancel a 1pt pip against one of the two −1pt pips, and you'd only now have to subtract 1 pip from your baby-pip count instead of having added 1 pip earlier and now subtracting 2.

In other words, while you should have countershifted the 4 pips instead of tracking them, the roofer leadoff exacerbated the problem—it squandered a later chance to cancel both the −3 three-prime and one of the near-side pips at the end.

This gives 3 + 5 − 3 = 5 and −5 pips.

Correct. The full tracking of your count is 3 + 5 − 3 = 5 supes, and +1 − 4 − 2 = − 5 pips. Without the roofer leadoff, your count could have been 5 − 3 + 3 = 5 supes, and −4 − 1 = −5 pips. Had you countershifted the 4 pips as well, you could have had 5 − 1 − 3 + 3 = 4 supes, and +1 pip. And with the best countershift (six-prime and two-to-S2, see this diagram above), the count was 4 − 3 + 3 = 4 supes + 1 pip.

In these comparisons, the "−3 + 3" looks like two separate counts but the consecutiveness of the offset helps. The more adept you become the more it feels like a 0 count or not counting at all.

5 is the same as 4(6) so 4(6) less 5 pips is 4(1). Naccel count for Blue is 4(1).

True, but in many or most cases, this is an unnecessary step. It is fine to leave it as 5(−5).

The main position is repeated below, with the point numbers labeled from White's perspective.

	4(1)

White: Two men on the [18pt] gives a count of 6.

Okay, at least you're starting with an integer. Still, it is better to first find a problem and fix it. The S3 checkers can be added in anytime, and it might end up better to include them in a larger formation later. (I mentioned two such examples in the fifth and sixth diagrams above.)

Move the checker from the [7pt to the 6pt] for a count of 1(1).

There you go with the fractional counts again. Rather than count this checker as 1(1) you would be better off counter-shifting the −3pt blot and one of the −4pt checkers back to the 0pt—i.e., getting them off the board and keeping your zero count ... well, I mean your 6 count that you started prematurely.

You seem to have adopted a methodology of starting with the back checkers first and working your way around the board. The reason you have developed this habit is that for traditional counting it is easier to count the big numbers first, and you also fear you'll forget something.

In Naccel, all the numbers are small, and there are a lot more checker-combining resources available through board symmetry. You are squandering most of these resources if you just clunk around, back to front. Instead, you should be looking to blow away as many of your checkers as you can with your first formation, anywhere you can.

The advantage of your approach is that you pretty much know what area of the board you're counting in next. But you're giving away too much in the process. Fixing this habit may take you out of your comfort zone (if it can be called that) and further slow your counts at first, but that will be a temporary effect and your counts will gather a surprising amount of speed before long.

The checkers on the white [−2pt and 2pt] cancel each other out.

This is okay, though it seems more natural to me to wipe out the entire five-prime with the +2/−2 pip shift I pointed out earlier.

If we move the checker forward one pip from the [−3pt to the −4pt] then we have a triplet on n−4 so that gives a count of −2 (plus 1 more pip).

The triplet is a good idea. A better execution, though, instead of your last step of removing the (Naccel) 2pt and −2pt, would have been to shift the 1pt spare back to the 2pt, and at the same time the −3pt blot to the −4pt, creating two triplets. These triplets could either be counted separately (+1 − 2 = −1) or viewed as a six-sym around the −1pt (faster).

In general, it is better to shift checkers than to adjust a running baby-pip count. Shifting will develop better habits; before long you'll be spotting bigger formations, more of your shifts will be dual purpose and you'll need fewer of them.

This leaves a final 3 checkers on the [1pt to move to the 0pt] (3 more pips). The count excluding pips is 6 + 1 − 2 = 5 and there are 5 pips to add so a Naccel count for white of 5(5).

Right. A count of 6 + 1 − 2 = 5 supes, and 1 + 1 + 3 = 5 pips.

You're improving. And, to be fair, you did better in the count of your second position of the same post; that's why I elected to comment on this one: I figured you'd learn more.

I hope that helps. You'll get there—stick with it!

Go on to Part 6.