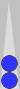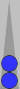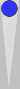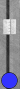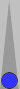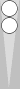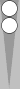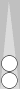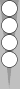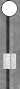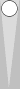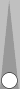|
This is Part 12 of the Naccel 2 series.
I'll start by reintroducing an old friend:
The midpoof was first illustrated (and discussed) in Part 6. The midpoof shown in the left-hand diagram arises more often than the midpoof in the right-hand diagram (shown for reference).
Next, I'll rehash two basic squads:
The left-hand diagram shows the most commonly arising triplet, having a count of 1. The right-hand diagram shows a pair, also having a count of 1.
Combining the triplet and pair produces this squad combination:
The formation on the left, combining the pair and triplet, is called a "chair," and the count is 1 + 1 = 2.
If
we replace the triplet 1 (on n2) with the triplet 2 (on n4), shown in
the right-hand diagram, we also have a chair. The right-hand chair has
a count of 3.
Moving
an entire squad or squad combination one quadrant alters the count by
the number of checkers in the formation. For example, let's look at the
same chairs located a quadrant lower:
The
chairs in the previous diagram pair counted +2 and +3; therefore, the
chairs in this diagram pair (five checkers, one quadrant lower) count
−3 and −2.
Chairs usually appear in the near-side quadrants, but they occasionally appear in the back quadrant:
These five-checker formations are two
quadrants higher than the original chairs shown of +2 and +3, so their
counts are ten higher: +12 and +13 (left-hand and right-hand diagrams,
respectively).
To
count any chair, take five times the nearest Super and add 2 (if behind
the Super) or subtract 2 (if in front of the Super). For example, the
chair above left is 2 × 5 + 2 = 12, and the chair above right is 3 × 5 − 2
= 13.
[Some alternative counting methods for the chair are: (a) Take five times the lower
Super and add 2 (when close) or 3 (when not close); or (b) Take three
times the nearest Super and add twice the other Super; or (c) Add your
known triplet and pair counts together.]
It
is easy enough to count a chair; nevertheless, I have found it
worthwhile to commit them to memory as instant counts, particularly the
near-side chairs of −3, −2, +2 and +3 (listed from left to right).
Chairs are useful counts on their own. They can also provide the basis for useful poofs; for example:
The S3 blot counts +3 and the chair counts −3. This six-checker formation is a "chair poof."
Next, let's discuss "shift-poofs." You can review one example in Part 5. Below is another example:
For
visualization purposes, the "roofer" (the checker on the roof) is
actually on a point to the left of S3. Therefore, if you shift the
roofer 1 pip to the right, it lands on S3. To keep the count the same,
you can countershift one of the n−4 spares to n−3. By doing so, you
achieve the poof in the right-hand diagram (same as the previous
diagram).
So ...
isn't the left-hand diagram already a poof? Yes, that's right! The only
difference between a shift-poof and a poof is that the latter is a
standard formation or one that you already recognize as a poof.
Consider the two poofs below. (And for variety, let's switch from Blue to White.)
As you know, a closed board (with or without checkers on S0) counts −5.
Okay, now: Any formation with a count of +5 can be poofed against a closed board.
In
the left-hand diagram, White has a pair of +5. This pair is sometimes
referred to as the "silver anchor" in backgammon. In combination with
the closed board (count of −5), I call the entire formation the "silver
poof."
In the right-hand diagram, White's midtriangle
counts +5, and so it poofs against White's closed board of −5 (which
is the same regardless of the presence or absence of checkers on S0).
Pop quiz: What is the count of the diagram below?
An easy way to count this is to shift the two n−4 spares to n−3, and
two checkers on n0 to n−1, thereby "closing" the board. It doesn't
matter that S0 ends up occupied by fewer than two checkers. Indeed,
even if S0 started with no checkers on it, you can freely conjure them.
The result of shifting is essentially shown in the previous (left-hand) diagram.
Okay, let's try another (requiring more imagination). What is the count of the left-hand position below?
While there are other ways of counting, try this long-range shift: double-hop
the roofer to the midpoint, and then (to offset) counter-hop the two bar point
checkers back to the midpoint. This gives you the mid-triangle poof in
the right-hand diagram.
Another way you can achieve poofs is with "motion" (movement/shift without equal countermovement). For example:
There
is more than one way to count the left-hand diagram, but a good, clear
way is to move the trailing checker 9 pips, thereby covering n1 and
creating a basic near-side poof. The movement of 9 pips can be thought
of as a hop of +1, plus a slide of 3 pips, for a forward motion of
1(3).
The result of the 1(3) motion is shown in the right-hand diagram.
You can also use partially offsetting motion (i.e., both forward and back). For example:
From the left-hand diagram, there are many ways to use partially offsetting motion. I'll list three:
- n7 to n2, and n1 (back) to n2
- n7 to n2, and n−2 (back) to n−1
- n7 to n1, and both n−2 checkers (back) to n−1.
These
motions are 5 − 1, 5 − 1, and 6 − 2 pips, respectively, for a net of +4 pips
in all three cases. The result of example (A) is shown in the
right-hand diagram.
It is also possible to combine shifting with motion. For example (from the left-hand diagram), you can:
- Move the midpointer down 4 pips and shift together the two blots.
- Shift the n7 and n1 blots a pip towards each other and move the trailing blot 4 pips (making the n2 point).
- Shift apart the n−2 checkers by a pip, and move the midpointer down 4 pips (in either order).
Either (a) or (b) achieves the right-hand diagram.
Of
these three options, (a) seems most natural to me. Also, the advantage
of (a) over (A) is that as you gain experience, you will see n−2 n−2
n1 n3 as a small (shift-) poof (equivalent to the right-hand diagram)
after the one-way motion of 4 pips faster than you'll see and account
for the two-way motion of 5 − 1 = 4 pips. In other words, (a)'s little
shift step will gradually decrease in mental impact and ultimately
you'll transcend (skip) it.
I'll
finish off here with my usual reminder: Motion (i.e., non-offsetting or
partially offsetting) is best used for leftover counts or to create a
position for which you can see that the remainder is exclusively
integer counts (preferably poof(s)). Don't get in the habit of using
non-integer motion or other leftover counting techniques more than once
during a count.
If
you find yourself using a lot of motion or multiple shifts to count a
single position, you're straining unnecessarily; I recommend that you
practice looking for Naccel formations that are more readily at hand.
Allow me to modify a line from a Moody Blues song: "They're all around
you if you can but perceive."
It's time for full board counting. Petter kindly supplies our first position:
All participants wisely chose to poof the n1 and n−1 blots and (of
course) the n0 point. For the remaining eleven checkers, Lucky Jim not
only found a fast way to count them, but he also summarized his count
efficiently: "m2+3 + Sym−1 + pair−1 = 3." (Bravo.) Those three
formations are shown separately below.
Jim's
first diagram is a straightforward midblot formation. "m2" means two
midpointers plus a blot on the second point after a Super. The "+3"
part identifies the relevant Super (in this case, S3).
Jim's second diagram is a sym around n−1, and his third diagram is a simple pair.
(Ian came up with the same correct count, except he subdivided the sym−1 (second diagram) into triplet−2 and triplet1.)
Let's have another look at Blue's position:
There is another counting method that is at least as fast. Remember the
midpoof? It is composed of two checkers on each of n−4, n−3 and the
midpoint.
If we remove the midpoof (as well as the small four-checker poof everyone else did), we are left with only five checkers to count:
This simplifies the count to: Mirror 2 + triplet 1 = 3.
Now let's repeat the position for White:
You can combine eleven checkers right away by shifting the two n−4
checkers back a pip and two n0 checkers forward a pip. That closes the
board (noting that it makes no difference whatsoever how many checkers
are or are not on n0) for a count of 5. Now that you've seen that
White's inner board is 5, you just look to create a +5 formation to
offset it.
In
achieving this offset, there are numerous solutions. The one that
occurred to me immediately is shifting the roofer 1 pip forward (to S3)
and the midpointer back 1 pip, like this:
Here, S3 + mirror = 5 offsets (shifted) closed board = −5. Poof! That leaves only the n8 blot, for a count of 1(2).
Note
that in the left-hand diagram I didn't actually illustrate the inside
shift to close the board, in order to more closely simulate over-the-board
practice. (After all, once you know the inside formation is 5, you
don't have to keep revisualizing it as a closed board.) Nevertheless, I
have bluntly added the right-hand (post-shift) diagram, for reference.
Let's revisit White's main position:
Another good solution is this motion poof:
Double-hop
(+2) the roofer to the midpoint, and back up the n3 checker to the
midpoint (−4 pips). This motion of 2(−4) is the entire count because
you end up with
The midtriangle (also summarized as m3+2), has a count of 5. It therefore offsets the −5 count in the inner board. Poof!
In
the right-hand diagram, the inner board is shifted and closed, for
further clarity. This midtriangle poof was diagrammed earlier.
Again,
the entire count of White's original position is the 2(−4) motion that
was used to create the midtriangle poof. [This count agrees with the
1(2) leftover count generated by the (1-pip) shift-poof method.]
Below
is another motion-poof solution, this time with one-way motion. From
White's original position, the roofer hops just once (+1) and the
midpointer moves +2 pips, which gives us
White's
freshly moved n13 and n5 blots are a rev 3,
while her n9 and n3 blots are (still) a mirror 2.
Together, their +5 offsets the −5 in the inner
board. Poof! (Again, the right-hand diagram includes the inside shift
as well, for complete reference.)
The entire count is the forward motion of 1(2).
Yet
another motion poof was produced by Petter. From the original position,
he moved the roofer 1 pip to S3 and the midpointer 1(1) to n0, for a
total of 1(2) motion, attaining this position:
[Note that this is effectively the same position reached in my solution. The difference is that I chose a 1-pip shift that isolated a blot having a leftover count of 1(2), whereas Petter used motion of 0(1) + 1(1) to actually put the blot onto n0.]
The
checker on S3 plus the outside mirror 2 cancels against the inner board
of −5. Poof! (If you scroll back, you'll see that's the way I counted
it.)
It
is interesting that (apparently) none of the participants noticed that
the inner board could be closed with a simple shift (whereas in the
past they've exhibited an awareness, eagerness even, to dunk this easy
−5 count). This suggests a subconscious resistance to breaking the
traditional 6pt (which in this case started with three checkers), but
don't worry; that mental block will evaporate before long.
So, how did
Petter count his post-motion position above? Answer: He poofed the S3
checker with the block −3
(consisting of two n−5 and two n−4 checkers),
and he poofed the remaining double-split −2 inside with the mirror +2
outside. Nothing wrong with that! Petter's entire count is his 1(2)
motion explained above the diagram.
Jim brings us our second position, shown below:
We'll start with Blue. When the count is this low, it is reasonable to
count forward to the bear-off tray: Motion of 3(5) gets the roofer to
the 2pt, plus 2 for the six-stack yields a count of 5(5).
However,
counting Blue to the bear-off tray means you either have to subtract 15
(which means you may as well count the normal way to begin with) or
count White to the bear-off tray as well (which wouldn't be efficient).
The dilemma exists only because it is so unusual to count a position
where one side has a lead this enormous, but we'll play along anyway.
Counting
the regular way (to n0), you can still start with motion of 3(5) but
then subtract the six-stack of −4, to get a difference of −1 pip. Then
subtract the 9 checkers borne off, for a count of −9(−1). This is
pretty much how Petter did it.
It
is also possible to count this position with minimal movement; just a
1-pip shift and a 1-pip (backwards) motion, in either order. Suppose we
start with the shift: enter the roofer to S3, and move one of the n−4
spares to n−3; that gives us
From
the left-hand diagram, −1 pip of motion gives you the chair poof in the right-hand diagram.
(The chair −3 poofs with the S3 checker.)
The −1p of motion, and −9 for the borne off checkers (not shown here), yields a count of −9(1).
Let's repeat the position with point-numbering from White's perspective:
Ian found a great solution: he shifted the n15 blot 2 pips to the left
and the n8 blot 2 pips to the right, as shown in the left-hand diagram
below:
The
n17 blot and n−5 spare create a mirror +2, plus the S3 checker gives a
count of 5, which poofs with the closed board of −5. (As always, the
presence or absence of checkers on n0 is irrelevant.) The only checkers
that contribute to Ian's count are the two on S1, for a total count of
2.
It
happens that the method I chose, shown in the right-hand diagram, was
nearly identical to Ian's. The difference: I countershifted S1 to n4
(instead of n8 to S1), creating a right-side mirror of 2. Since all
else poofs (as before), the total count is 2.
Below is another shift that works well. From the original position, the S3 and n15 checkers move a pip closer to each other:
In
the left-hand diagram, the just-shifted blot on n16 and the blot on n8
form a reflection (around S2) with a count of 4. Add the S1 checker
for 5, poofing with the closed board of −5. All that remains is the
mirror (formed by the new n17 blot and n−5 spare), the entire count of
2.
Incidentally,
it is equally good to countershift n8 instead of n15, as illustrated in
the variant (right-hand) diagram. That creates a reflection 4 composed
of n15 + n9 (instead of n16 + n8).
Note
the marvelous efficacy of dual-purpose shifts. In the two (similar)
cases above, the (1-pip) shift yields a mirror and the (1-pip)
countershift yields a reflection.
Petter's
shift involved more movement, but he attained an even cleaner position:
He shifted S3 to n15 and n8 to S1—a total of 5 pips, and
countershifted n−5 to n0, thereby reaching
On the left is a silver poof, which is a cancellation of a pair +5
with a closed board −5. The two checkers on S1 are the entire count of 2.
Finally, I want to reiterate my thanks to Matt Ryder for his excellent work on Naccel-numbered diagrams
(which anyone can now create), and to Ian Shaw for showing me the ropes
for formatting side-by-side diagrams. These two elements have made it
possible to offer much more lucid explanations and presentations.
| 




![]()