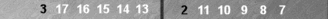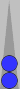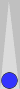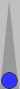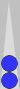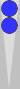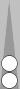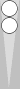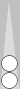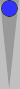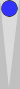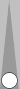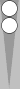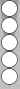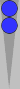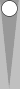|
This is Part 9 of the Naccel 2 series. In this post, we'll dive into variants of the basic squads. Squad variants are simple to learn and often save you a step shifting within quadrants.
The basic squads are six-stacks, triplets, pairs and blocks.
To
count two checkers on any point, divide the point number by 3. When the
two checkers are on the middle point of a field (halfway between two
Supers), their count is an integer and they are considered a "pair." An
example is shown below.
This pair is on n3. It can be counted as a third of its point number (a third of 3 is 1) or as the sum of its flanking Supers (0 + 1 = 1). Perhaps some of you by now simply recognize this pair as an instant count of 1, and that's the fastest way to count it.
Let's see what happens when we pull these checkers apart, moving them a pip in opposite directions:
This formation is called a "split" (short for split pair). Clearly, it
has the same count as a pair, because you can shift the checkers
towards each other to form a pair. The split diagrammed above has a count of 1.
We can further separate the checkers, as follows:
This formation is called a "wide" (short for wide split or wide split
pair). You can shift the checkers towards each other to form a split or
a pair, so naturally it has the same count. The wide diagrammed above
has a count of 1.
You can double or triple the height of the pair, split or wide as follows:
The right-hand diagrams are easy to count as syms (six-syms). The point
of symmetry in all cases is 3, so the count is 3.
So, you needn't worry about counting them as triple-sized squads, though the pattern connection is worthy of note.
To
count the four-checker formations in the left-hand diagrams, you can
add the point numbers and divide by 3. So the counts of the three
diagrams are (3 + 3) ÷ 3, (2 + 4) ÷ 3, and (1 + 5) ÷ 3, respectively: in all cases
it's 2. Or, if you recognize the two-checker formations as being 1,
double that to get 2. (Yet another way is to double the sum of the
flanking Supers: (0 + 1) × 2 = 2.)
To make it as tricky as possible, let's count a double split in the back quadrant and also reverse colors:
To count White's double split, you can add the point numbers and divide
by three (16 + 14) ÷ 3 = 10, or you can double the sum of the flanking
Supers (3 + 2) × 2 = 10 or similarly shift to the Supers, or you can shift
it to a double pair and count it (15 ÷ 3) × 2 = 10, or if you know the
single pair is 5 then count the double pair as 5 × 2 = 10. Or, finally,
you can commit this double split to memory as an instant count of 10
(as I have).
For completeness, let's look at a common double wide, again for White:
To count White's double wide, you can add the point numbers and divide
by three (−5 − 1) ÷ 3 = −2, or you can double the sum of the flanking
Supers (−1 + 0) × 2 = −2 or similarly shift to the Supers, or you can shift
to a double split (−4 − 2) ÷ 3 = −2 or double pair (−3 − 3) ÷ 3 = −2, or know
that whatever you're shifting to counts −2, or commit to this double
wide to memory as an instant count of −2 (as I have). So many options.
Next, let's review the "triplet."
This triplet is on n2. It can be counted as half of its point number: half of 2 is 1.
Or, you can shift two checkers to the nearest Super and the third
checker to the second-nearest Super, effectively counting it as 0 + 0 + 1 =
1. Better yet, no doubt some of you already recognize this commonly
arising triplet as an instant count of 1.
If we pull this triplet formation slightly apart, we achieve ...
This formation is called a "layer." It counts the same as the central
point number (n2 in this case) divided by 2, so this layer counts 1.
By shifting it back to the triplet (or shifting the two left checkers
to S0 and the right checker to S1), this is easy to verify.
You can double or triple the height of the layer as follows:
The formation in the left-hand diagram is a double layer; it is twice a
layer of 1 and thus has a count of 2. [It also happens to be a commonly
occurring sym called a three-prime. As with any other sym, its count is
the same as the point number at the center of symmetry; the central
point is n2, so the count is 2.]
The
right-hand diagram is a triple-layer. It can be viewed as thrice a
layer of 1 for a count of 3. [Alternatively, it can be viewed as the
three-prime (in the left-hand diagram) with a count of 2 topped off
with a layer of 1, another way to get the correct count of 3.]
Here is another example of a triple layer:
For texture/orientation, I've added two checkers on the S0 point. (As
the S0 point is irrelevant, it could also have three or four or five or
however many checkers you like on it, including one or zero, and the
same count would hold.)
This
triple layer is thrice a layer of −1, for a count of −3. Or, it is a
layer of −1 atop a three-prime of −2, for a count of −3. Or, by
shifting the n−3 and n−1 three-checker points towards each other, you
could even treat this formation as three triplets stacked up on n−2
counting −1 each (total of −3).
The
other squad variant of a triplet is called a "wedge" (first introduced in Part 4). If you
asymmetrically shift two checkers of a triplet one pip, and the third
checker two pips in the opposite direction, it results in ...
This wedge can be counted as the "in-between" point (the one on which
the shifted triplet would reside, which is n2) divided by 2—that
yields a count of 1. Until you've gained confidence with this formation
being an instant count of 1, you can shift it inwards to the triplet
(or layer) for a more obvious count of 1, or shift it to the Supers as
0 + 0 + 1 = 1, or even count it forward to S0 as 4 + 1 + 1 = 6 pips = 1 supe.
You can double the wedge, as shown below:
This double wedge yields a count of 2, either by thinking of it as one
wedge (of 1) on top of another, or by shifting it to the Supers, or by
shifting it to a three-prime sym around n2.
There is a similar but converse wedge formation in the outer board. It's single and double versions are:
The
formation in the left-hand diagram is the flip-flopped version of the
first wedge. It was created by asymmetrically shifting a triplet on n4
and its count is therefore 2, the same as the n4 triplet. You can also
shift it to the Supers, for a count of 0 + 1 + 1 = 2.
The
formation in the right-hand diagram is a double wedge, and counts 4. It
is twice the size of the wedge (in the left-hand diagram). To reach the
same correct count, you can shift either to the Supers or to a
three-prime sym around n4.
Next, we'll review the "block" (first introduced in Part 6).
In
the left-hand diagram, the basic "block" is shown, which occurs, for
example, after an opening 61. To count a block, add the point numbers
and divide by 3. Thus, this block, occupying n1 and n2, counts (1 + 2) ÷ 3
= 1. By now, many of you already know this block as an instant count of
1.
In
the right-hand diagram, for reference, I have diagrammed a "double
block." This does not arise frequently, but it's very helpful to
recognize when it does (or you can shift to it when you're close). The
double block's count is twice that of its underlying block, naturally.
Let's switch colors to White and show a block in the back quadrant:
To count any block (or for that matter any two points), add the point
numbers and divide by three. Here, (17 + 16) ÷ 3 = 11. Alternatively, you
can shift one point to S3 and the other to create a common pair on n15,
for a count of 6 + 5 = 11. That said, it is useful to remember this
formation as an instant count of 11.
If,
from the second point of a block (the one not adjacent to the Super),
you shift a pip in each direction, you create a squad variant of the
block called a "triangle." It is shown below.
The triangle can be shifted to a block and counted the normal way (add
the points and divide by 3, yielding 1 here), or it can be shifted to
the Supers (0 + 0 + 0 + 1 = 1 in this case), or it can be counted forwards as
1 + 1 + 1 + 3 = 6 pips = 1 supe, or it can be instantly recognized as a count
of 1 (always the fastest way).
Below are two examples of a triangle as it appears in other quadrants:
The
triangle in the left-hand diagram occurs when a player runs a checker
out two pips shy of his midpoint. (If his midpoint has more checkers,
you can still allocate three of them to count this formation, and count
the remaining midpoint checker(s) in a separate formation.) You can
shift this "midtriangle" to the "midblock" for a count of
(8 + 7) ÷ 3 = 5,
though as a triangle it arises often enough you will hopefully know it
as an instant count of 5 before long.
The midtriangle is also considered a midblot formation of three/third + S2 = 5. While seemingly redundant, the more reference points you have for recognizing and counting a formation, the better.
In
the right-hand diagram, there is a triangle in Blue's back quadrant.
Note the similarity to White's block diagrammed previously. You can
either shift this triangle to a block and count it as 11, or shift to
the Supers (S3 × 3 + S2 = 11) or even learn it as its own 11 count.
The final squad I'd like to show you is the "sock." Although I am illustrating it for the first time amidst a series of squad variants,
the sock is in a sense just as special as the pair (two-checkers),
triplet (three checkers), block (four checkers), or stack (six
checkers), because it is the only basic squad composed of five
checkers.
You can count this sock by shifting (conjuring if necessary) an S0
checker and the n2 blot inwards to create a six-stack on n1 (count of
1), or by shifting outwards to a block (count of 1)—i.e., one
checker back to n2 and another forward to S0 where it disappears.
Alternatively, you can shift to the Supers (0 + 0 + 0 + 0 + 1 = 1), or you can
count it forward to S0 as 1 + 1 + 1 + 1 + 2 = 6 pips = 1 supe.
You
have to be careful when you shift on and off Supers. Any checkers
shifted to or from S0 count zero and are therefore irrelevant, but if
you're making similar shifts to a different Super, add the
count of that Super for each checker added there, and subtract the
value of the Super for each checker conjured from there.
For example ...
Here, you can shift a midpoint (n7) spare forward to S1 and another
midpoint spare back onto the n8 blot, creating a midblock with a count
of (8 + 7) ÷ 3 = 5, plus 1 for the new S1 blot, for a count of 6.
Alternatively,
you can count this sock by shifting the blot to n7 (the midpoint) and
countershifting/conjuring a checker from S1 to n7. That gives you a
six-stack on n7 for a count of 7, but be sure to subtract 1 for the S1
checker you conjured, thus giving you a net of 6. [In essence, you had
to back-hop a (freely conjured) checker from S0 before shifting it to
n7, and that back-hop carries with it a count of −1.]
Personally, I find this sock easiest to count as a midblot of four/fourth + S2 = 6.
Or, rather, that's the way I used to count it before it sunk in as an instant count of 6.
Let's try switching from Blue to White, and also hop the blot back to the back quadrant:
This formation is no longer a sock, but you can hop the blot +1 to
morph it into a sock and then count it however you would choose to
count the ready-made sock in the previous diagram. Here, you can count
White as +1 (hop) + 6 (midsock) = 7.
Alternatively
(and preferred, in my opinion) is to count White's formation as a midblot:
Four/fourth + S3 = 7.
(Note that over the board if the blot doesn't happen to be in the ideal spot, you can always shift it.)
Stacks,
pairs, triplets, blocks, and socks: you are now more or less familiar
with them all. These basic squads, and their variants, can also be
combined (which we may look at another time); or they can be offset,
thereby giving you "squad poofs."
Below are a couple common examples of squad poofs. I'm moving them to White's side, for more practice with that color:
The
squad poof in the left-hand diagram can occur in two rolls by White
(with double 4s and 1s, or double 3s and 2s, played offensively),
though there are many other ways for it to come about. With the S0
checkers being irrelevant (as usual), White's −1 block offsets her +1
triplet, making her entire near side go "poof"!
There
is another squad poof in the right-hand diagram. This might come about,
say, if White rolls 61 and 55, or 53 and 66. (As always, the number of
S0 checkers is variable.) This one is a (negative) pair cancelling out
a (positive) block.
In
summary, in the left-hand diagram White has a block/triplet poof, and
in the right-hand diagram she has a pair/block poof. Completing the
round robin, an example of a pair/triplet poof can be seen (for Blue)
in Part 4.
Whew! You still with me? Congratulations; I'll reward you with some full board positions to count.
Our
first position arose in Stick Rice's thread "Live by the Sword." The
original checker colors were Yellow and Brown, but I translated them to
Blue and White at the bottom of my reply post. In other replies of that thread, you can see how people counted the position.
I am also including the position here:
For Blue, all participants poofed the S0 checkers and counted the sym around n3 as 3. Only five checkers remain:
There are at least three ways to count these five checkers. Jim chose
to shift the midpoint forward and the n−1 point back, counting S1 × 2 =
2, plus 2(4) for the blot.
Petter counted the same way, except (evidently) he already recognizes the point diag of midpoint plus n−1 as a count of 2 without shifting.
Ian counted the far side as 5. Parenthetically, he mentioned shifting to S3
+ S1 × 2, though as a midblot you can count it without shifting as
two/second + S3 = 5.
Then he subtracted the 2 pips on n−1.
Ian's far-side shift isn't necessarily better or worse than Jim's mid/near
shift, and the (no shift) midblot two/second + S3 minus 2 pips seems no
better or worse than Petter's (no shift) point diag 2 + 2(4), but I am
pleased to see the variety.
Counting these five Blue checkers as such, and adding 3 for their n3 sym (see
outer board of previous diagram), gave Jim and Petter 7(4) and Ian
8(−2), either of which is a correct count. High marks are deserved all
around.
Let's repeat the main position, numbering the board from White's perspective:
For White, Jim, Petter and Ian counted identically: Shift the n2 point
to n1, poofing it with n−1, and countershift the two n16 spares back to
n17. That's a block of 11, plus 4 for the midpoint mirror; total of 15.
Beautiful.
[Note that in creating the little poof around S0, shifting n−1 to n−2 is just
as valid as shifting n2 to n1 (or you could even move one checker 1 pip
from each point, creating a four-blot poof), though the eye tends to
spot the tighter poof more often.]
I'll repeat the position for White so that my two paragraphs beneath will be easier to follow:
It is worth mentioning that without shifting, you can count: (a) two
back checkers plus n−1 as a zag = 5, (b) the other two back checkers
plus n2 as a "rev" = 6 (reverse diagonal, I believe the only mirror
variant I have not yet shown you), and (c) midpoint mirror = 4. Adding
them up, 5 + 6 + 4 = 15. But I consider the n2 and n16 left-shift to be
at least as fast, leaving (0 +) 11 + 4 = 15.
The
fastest count I know for White is (no shift) near side = 2, far side =
13. Her near side you will recognize as a sym around n2. Her far side
is a "midfour" you don't know yet (fairly uncommon). [You can fake the
midfour by shifting n16 back and n7 forward a pip, to get block 11 +
(S1 × 2) = 13, but overall that would be a beat slower than the other shift
the participants found.]
Our second counting position comes from Timothy Chow's post, White to play an awkward 2-1.
Petter was first to rise to the task this time. For the Blue count, I
was impressed to see him shift the n−5 checkers back to n−3 (for a triplet/pair poof) and
countershift the four midpoint checkers down to S1, for a count of 4.
That takes care of all the checkers except for the one on S3. Total count is 7.
Petter's count was my choice as well, except for the countershift I moved two
midpointers 2 pips each, creating a mirror = 4. I find it slightly
easier, when possible, to shift and countershift the identical number
of checkers and pips, though either way seems to me to stand out above
other counts of this position; it's hard to beat large-scale poofs.
Jim
and Maik counted S3 as 3 and the triplet on n2 as 1; that's 4 so far.
The S0 checkers are invisible, so these six checkers are left:
Jim found a clever way to count these six checkers: He moved two of the
midpointers down 1 pip (to S1) and the other two midpointers down to
n5. This is an unusual though acceptable hopping maneuver: a combined
movement of 6 pips. The resulting n5 point poofs with n−5. For
counting, the amalgamated 6-pip "hop" is +1, and S2 × 2 is 2, for a count
of 3.
Maik
noted: "There seem to be a million ways to count the checkers on n7 and
n−5. I like the hopping approach: Hop all of them to n1 (that's 4
forward hops and 2 backwards hops netting +2) to get a sixtuplet worth
1."
Quite
right; there are a seemingly endless number of ways to count these six
checkers. (Jim's amalgamated 6-pip hop and Maik's meet-in-the-middle
hops are just two.) Easiest, perhaps, is to hop just two of the
midpointers to n1, creating a long-range sym around the n1 point; i.e.,
+2 for the hop plus 1 for the sym.
Recapping
the count of the main position, S3 = 3, the triplet is 1,
and the six checkers in the above subdiagram count 3, for a total of 7. That agrees
with Petter's count (and mine) of 3 + shift/poof + 4 = 7.
I'll repeat the position from White's point of view:
For White, Petter shifted the four back checkers toward each other to
n15 for a double pair that he knows as an instant 10. The triplet is 1,
and he shifted the three rightmost checkers to meet on S1 for another 3.
Adding them up, 10 + 1 + 3 = 14.
Maik shifted White's back checkers as Petter did, except he counted the
resulting four checkers on n15 not as a double pair, but instead as a
double zag with S0(!)
Both ways yield 10 for the left side, except that
Maik "counted" all eight checkers (ignoring the fifth one on S0),
whereas Petter counted only four (ignoring all five on S0). In both
cases, one left-side formation is being counted.
Jim counted the right side as Petter did. For the left side, though,
instead of shifting White's back four checkers to a
double pair, he
zagged (−1) the n14 point back to n17, creating a n17+n16 block that he
knows instantly as 11.
Like
Petter and Jim, Maik counted the n2 triplet as 1, but (in my opinion) Maik
improved on the count of the three checkers on the far right by
counting them as a midblot Two/second + S1 = 3.
Up to this point, I have been writing the
midblot formations longhand in
order to include the reminder that two checkers on the midpoint plus a
blot on the second point of the field (counting from the Super as the
zeroth point of the field) are involved, but henceforth I am switching
over to the shorthand "midblot 2 + S1" that Maik himself used. (Later,
I might even shorten it to mb2+1, the way I write it for self-notes.)
Excellent,
everyone. Here is a potential improvement, though: the back checkers
are, where they stand, a "double split" of 10, as illustrated earlier
in this post.
In other words, you can count White's position quickly as 10 + 1 + 3 = 14
without
shifing or zagging. However, this is only of use once you have learned
the (relevant) instant counts; until then it makes sense to employ
motion for one or two of the three formations as Maik, Petter and Jim
did.
There are two further "potential improvements." The first is to count White's
entire right side as an instant 4, which I did, only by familiarity
gained through repeated practice.
(The n2 triplet started as an add-on
count to other formations and eventually merged for me.) The other is
in seeing the entire position as an instant 14; I'm not there yet (and
I might never be)—I still have to add the left and right sides of
White's position above as 10 + 4. Pathetic, eh?
Finally,
Petter suggested a third position to count, which had appeared on Phil
Simborg's site as "position of the day" on February 3rd:
Nobody else got around to posting their count, but Petter did a great
job. For Blue, he poofed the entire near side, leaving only the two
checkers on S2, for a lightning count of 4.
Let's repeat the diagram with point-labeling from White's point of view:
Petter noticed that White's near side is also a poof. My guess is that
he shifted the spare from n2 forward and the spare from n0 backward to
fill in the n1 point (creating the obvious
five-prime poof), but
possibly he already he knew it directly as a block/triplet poof poof.
That
leaves only five White checkers to count: Petter noted that the
midpoint is 4(4) and the blot is 2(4); he totalled these to 6(8) =
7(2).
When
possible, I avoid adding (or subtracting) mixed supe/pip counts, though
I have to admit that Petter's count here is fast! Still, even faster, I
believe, is to move the blot 2 pips forward, which gives us ...
Adding this known midblot 4 + S3 = 7 (an instant count for me) to the
+2 pips (moved) yields a White count of 7(2) in the main position.
Go on to Part 10.
| 


![]()