Summary of Sho's Pip Count, "Five-Count"

Created by Sho Sengoku, 2001

Key Concept of "Five-Count"

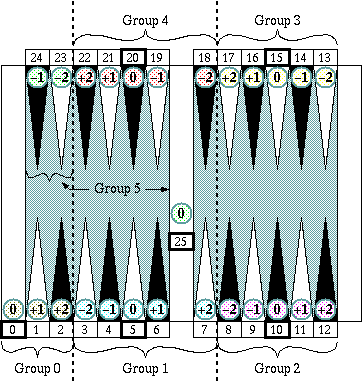
By grouping all 26 points, including the 0 point (the goal) and the 25 point (the bar), as shown in Diagram 1, each group can have five points (or three points) with 5n (n = 0 ~ 5) point at a center of the group.  Any point on the board can be described as a 5n+e (e = −2 ~ +2) points.

Given group numbers as shown in Diagram 1, number of checkers in a group times group number gives 1/5 of pip count of checkers in the group with errors caused by checkers placed on points left or right of the 5n point, the center of the group.  Performing the same process for each group and summing up the results is called a "group counting", and the result of multiplying the group count number by 5 is called a "rough count number".

An exact pip count is derived by eliminating those errors from the "rough count number", and this process is called an "adjustment" in this system.

Key concept: Six groups, −2 ~ +2 error range in a group [Diagram 1]

Group counting process

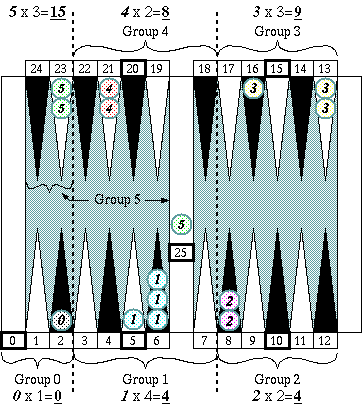
To get a group count number, count number of checkers in each group and multiply the number by the group number, then sum up all group numbers from Group 1 to Group 5. In this example, the grout count number is 40.

Group counting:  0+4+4+9+8+15 = 40 [Diagram 2]

Adjustment process

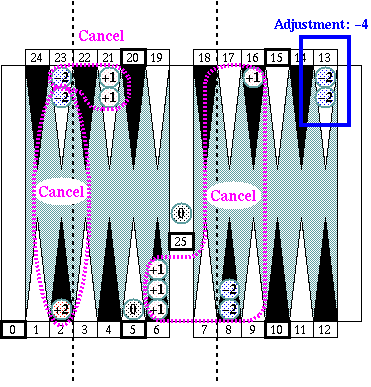
By multiplying the group count number 40 by 5, we get the rough count number 200. Canceling as many errors as possible gets us −4 as the adjustment number of the position, and we get the exact pip count of the position 196 (= 200 − 4.)

Adjustment: −4 [Diagram 3]

Characteristics of the system

1. Takes advantage of the symmetric nature of the board

All group center points, 0, 5, 10, 15, 20, 25 point, are located symmetrically.  By taking advantage of this symmetric nature of the backgammon board, grouping is done by simply placing two boundary line, one between 2 and 3 point, another between 7 and 8 point.

Also, alternately colored points of the backgammon board well support an adjustment process. They distinctly separate −2, −1, 0, +1, +2 error points in an adjustment process of the system.

2. Lowers numbers in a counting process

The grouping keeps all numbers in process lower, and therefore the system rearly requires arithmetic operations between big numbers.

3. Uses base number 5

Decimal is the system we use in a daily life. The base number of this system, 5, is a half of 10, and therefore is very easy to use. In order to get a rough count number after a group counting process, all you have to do is multiply the rough count number by 5, or multiply it by 10 first then divide it by 2.  That's much easier process than using base number 3 or 6.

4. Minimizes arithmetic process

Using the backgammon board as an counting tool, the system minimize needs of  arithmetic process by a human brain.

Finding 10s in both a group count and an adjustment process reduce your arithmetic tasks, and it is quite easy to find 10s in the both process. For example, in a group count process, two checkers in Group 2  (2x3) and two checkers in Group 3 (3x2)  make 10 together.  In an adjustment process, five checkers on the midpoint (−2 as an error number for a checker) make −10 as an adjustment process.  Adding or subtracting 10s (10, 20, 30...) is a very simple task, because all you need to do is increase or decrease the second digit of the number in process (sometimes it affects the third digit though), and you don't have to worry about the first digit of the number at all.

Cancellation process in an adjustment process doesn't require any arithmetic process, if you know 1 − 1 and 2 − 2 are both zero.

And assuming you subtracted or added 10s in an adjustment process prior to error cancellation task, an adjustment number always should be smaller than 10 or bigger than −10 (−9 ~ +9).  Adding or subtracting that kind of small single digit number from the number in process is an EASY math for a human.

5. Requires no "mental shift"

Many other pip counting systems require "mental shift" during the process. That should be quite burden for most people, and often cause of a wrong count.

This "Five-Count" system doesn't call for any mental shift.

6. Easy and quick to master

Ten or fifteen minutes to understand the system. A half or one hour to become able to use the system in a real game. One or two days to master the system completely. (No scientific proof for this estimate is provided :-)

7. Easy and quick to count

Because of the reasons explained above, this system is easy and fast.

8. Reliable counting

And less chance to make a wrong count because of all the same reasons. Very reliable counting.

Continue on to:   Part 1: Quick View: Introduction to "Five-Count"

Sho Sengoku's Five Count Overview:   Summary of Sho's Pip Count, "Five-Count" Part 1:   Quick View: Introduction to "Five-Count" Part 2:   Techniques for Easier and Faster Counting Part 3:   Practice, Practice, Practice Part 4:   Even Faster! Part 4.1:   Common patterns for "10s" in group counting Part 4.2:   To get a "rough count" even faster Part 4.3:   Common cancellation patterns in an adjustment

 

See:  Other articles by Sho Sengoku

See:  Other articles on Pip Counting

Return to:  Backgammon Galore : Articles