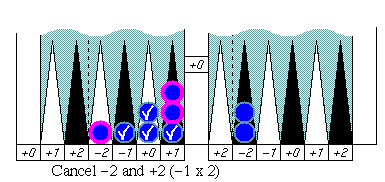Always try to find 10s (10, 20, 30, ...) in both a group counting
process and an adjustment process. Adding or subtracting 10s from
any number is quite easy because all we have to do is increment or decrement
the second digit of the number in process.
See how easy it is to subtract 10 from 125 for example.
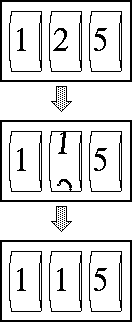
We (usually) don't have to carry over or borrow down any numbers.
All we have to do is just roll down the second digit drum by one in our
mind.
Example 1. (in a group counting process)
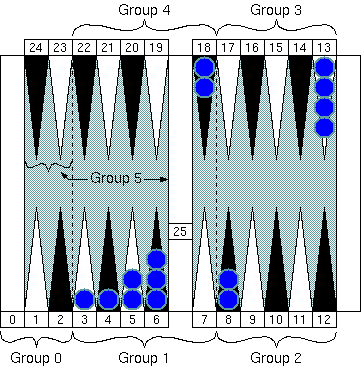
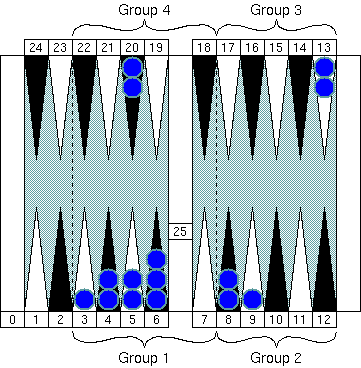
We have 7 checkers in "Group 1" (1 × 7 = 7), 2 in "Group 2" (2 × 2 = 4), 4 in
"Group 3" (3 × 4 = 12), and 2 in "Group 4" (4 × 2 = 8.) Before we start adding
all those numbers, why don't we check it again if there are any 10s here.
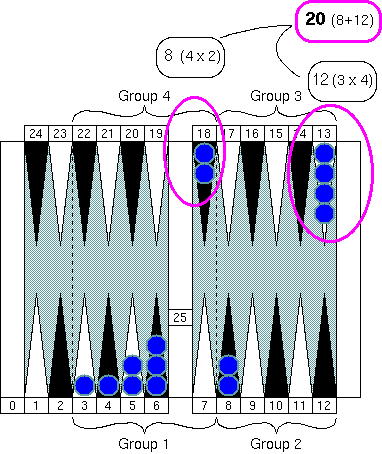
The two checkers in "Group 4" and the four checkers in "Group 3" nicely
make 20 together.
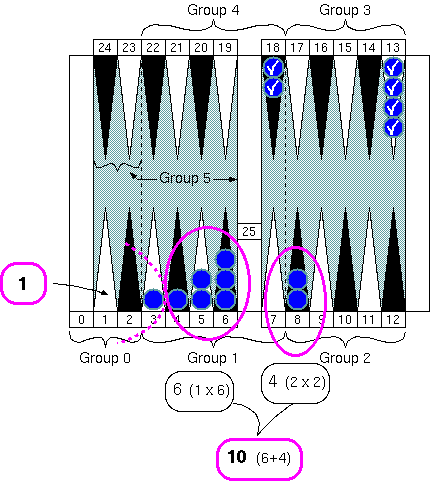
If we put aside one checker on the 3 point in "Group 1", we have 6 checkers
in the group, which make 10 with two checkers in "Group 2."
Then we have
1 for the checker we just put aside.
Now we have 20, 10, and 1 to sum up. The total group count number
is easily calculated as 31. Rough counting number of 31 is
155
(= 310 ÷ 2.)
Example 2. (in an adjustment process)
Using the same example we have just used above, we will see how "finding
10" speeds up an adjustment process.
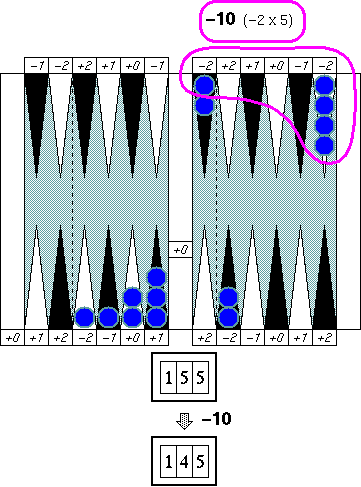
Before we start cancellation it is always good idea to seek for any
convenient 10s if there seem to be unbalanced numbers of "−2"s or "+2"s.
In this example there are many "−2"s and no "+2". Picking up five
"−2"s makes −10 that we wanted. Subtract 10 from (or add −10 to)
the rough counting number 155.
Now we have 145 as a new rough counting number. We then start
a cancellation process with much fewer checkers to take care of.
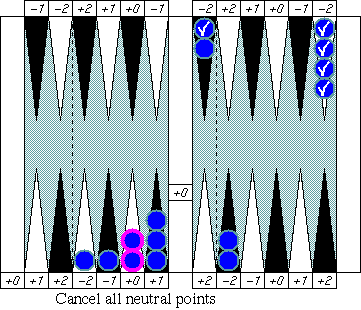
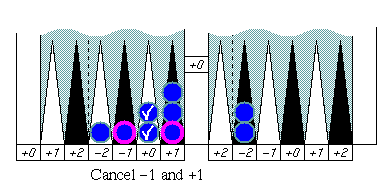
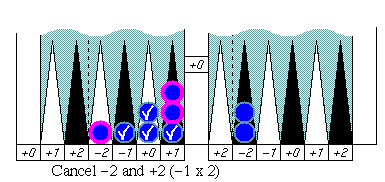
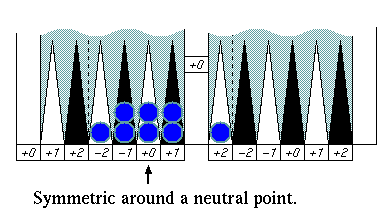
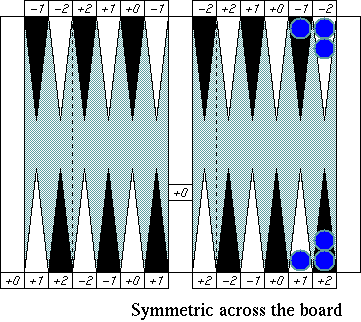
There are three major symmetric patterns that cancel error
numbers all together at once in an "adjustment" process. Finding
those symmetric patterns simplifies and speeds up your pip counting.
Pattern 1
Pattern 2
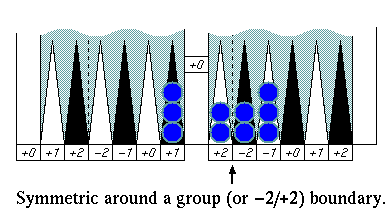
Pattern 3
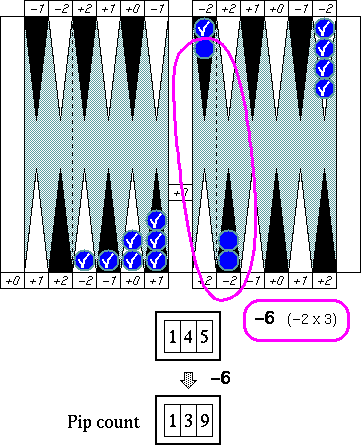
Example
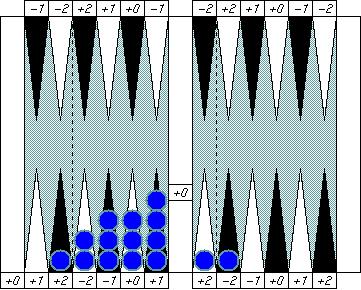
This is a common bear in position you may have seen in real games.
The group count is 15 (13 in Group 1, and 1 in Group 2), so the rough
count of the position is 75 (150/2). Now, do you see a symmetric
pattern here?
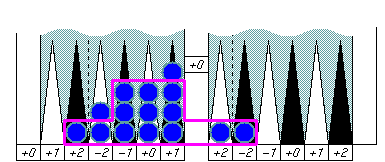
This "symmetric around a neutral" pattern cancel all errors by 13 checkers
at once, and we've already got an adjustment number −1 (= −2 + 1) that makes
the pip count of the position 74 (= 75 − 1).
In a group counting process, sometimes total group count
number is already divided in two and you get a "rough counting" number
immediately. For example position like this:
You can make a group count in a straight way and get 28. You then
add one more 0 (zero) to the right of the number (280) and divide by 2
to get the rough counting number. But if you look at the position
more carefully, you can find two "14" group counting numbers.
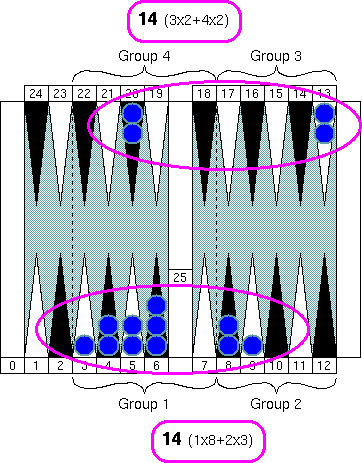
You've automatically got the rough counting number without dividing
by 2, because they are already divided by 2. The rough count is 140.
Then you can proceed to an adjustment process.
And, in a second, I get the final pip count 130. How did
I do it?
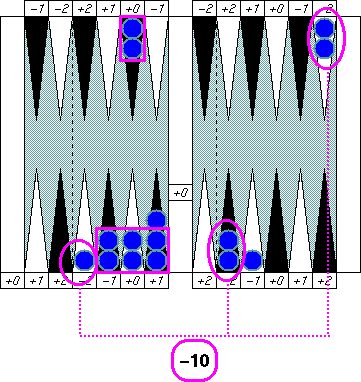
Do you see how I finished the adjustment process for the position literally
in a second?