Common cancellation patterns in an adjustment

Five-Count Part 4.3:
Common cancellation patterns in an adjustment

Created by Sho Sengoku, 2001

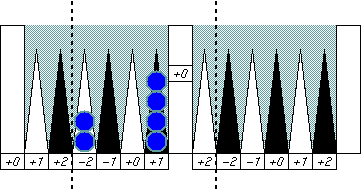
Five in a row

Checkers lined five in a row cancel all their error counts no mater where they are. This is because any five consecutive points have all different error numbers from -2 to +2 but no duplications.
Check yourself about this, and you will understand that a five point prime in any location cancels all error numbers in it at once.

Weak symmetric patterns

Not exactly symmetric, but you can see they are "balanced" on the group center (the 5 point in this example.) A balanced pattern on a group center always cancel its error numbers.
This pattern is very common and you will often see the same pattern in a real backgammon game.

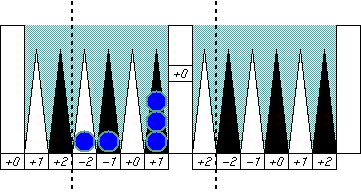
The same "balanced" pattern, and it cancels all errors at once.

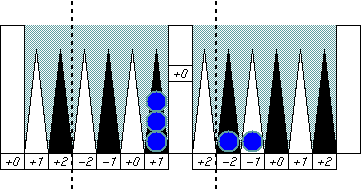
Not balanced as it is, but it would be balanced on the 9 point (the center of Group 2) if the three checkers on the 6 point were the 11 point.
Or you can think that it is a weak symmetric around a group boundary and cancels all error numbers at once.

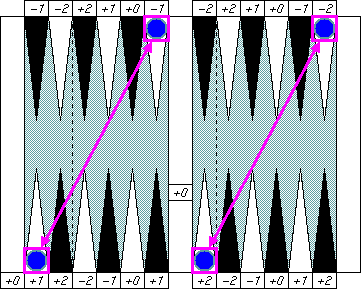
Diagonal corners in a box

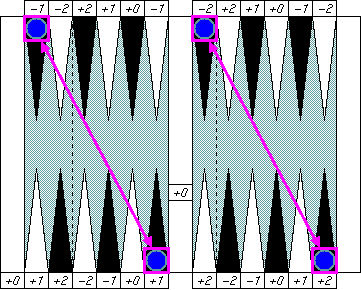
Any pair of checkers on diagonal corners of the left side or the right side of the bar cancels error numbers together.

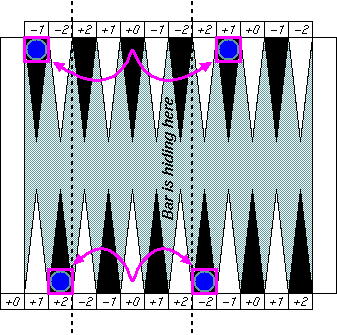
Distant symmetric patterns

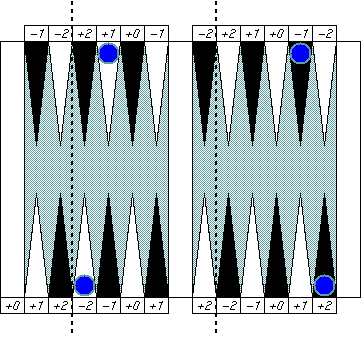
This "distant symmetric" pattern may be a bit harder to catch at a glance. That's partly because they are many pips away, but mainly because the bar cuts off the board in two and change our perception of distance.
If you removed that big bar form the board view, then you could easily see good symmetric patterns.

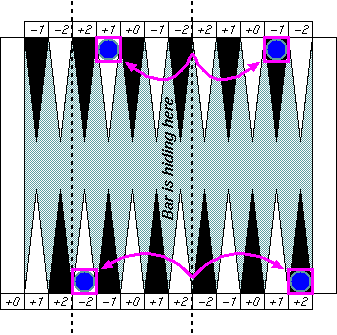
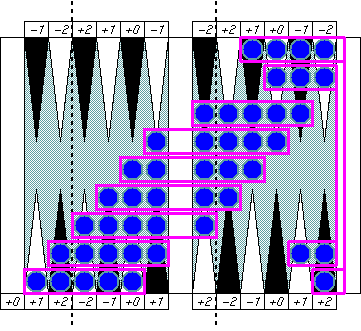
You can't just erase the bar from a real backgammon board of course.
If you don't like this "fake" board image, then just compare two checkers' locations in the group boxes, and you may find symmetry there.