Five-Count Part 1:
Quick View: Introduction to "Five-Count"

Created by Sho Sengoku, 2001

1.0.  Step 0: Basic Idea: Grouping

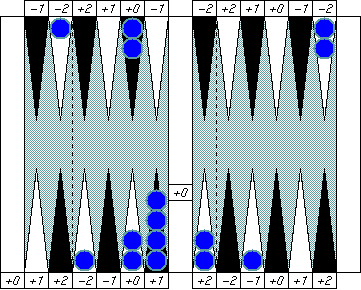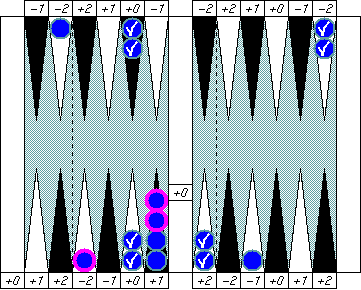
What is Blue's pip count? That's 5, right?

---

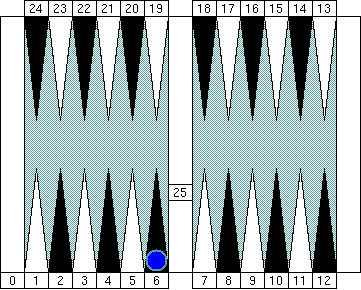
How about this one? You might say "Blue's pip count is 6." That's perfectly correct of course, but there's a better way to call it. Instead, try this way: "Blue's pip count is (5+1)."

---

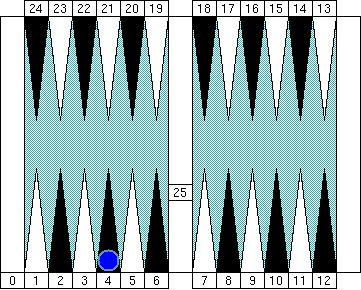
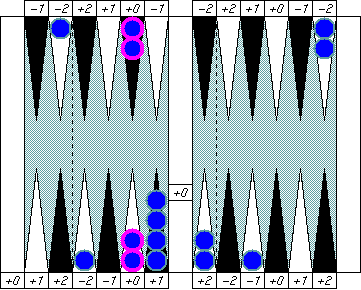
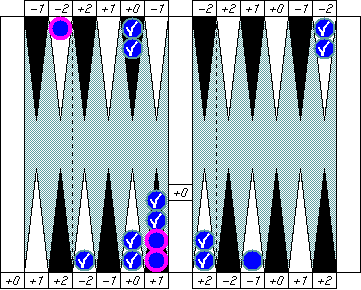
In the same way, read this one as "Blue's pip is (5 − 1)" instead of "Blue's pip is 4." We'll see great advantage of this notation soon.

---

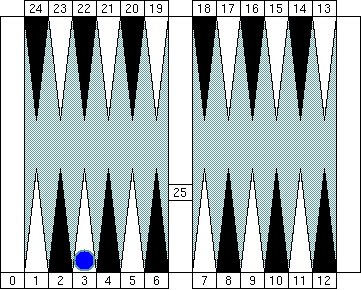
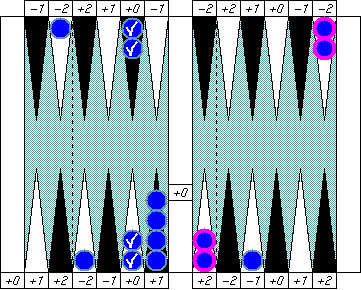
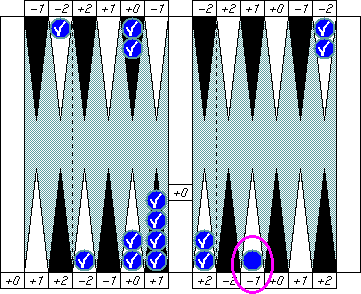
Blue's pip is (5 − 2).

---

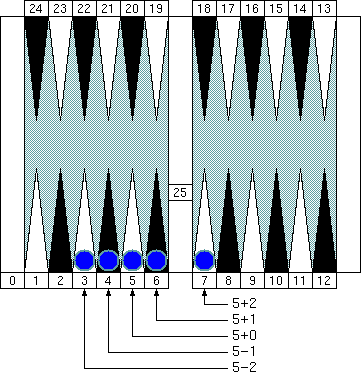
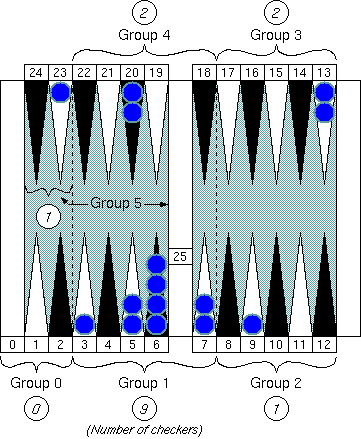
As we have seen, we can think of these points as a member of the "5 point family." For now, we close our eyes to those +2 to −2 differences. Let's call this family "Group 1."

---

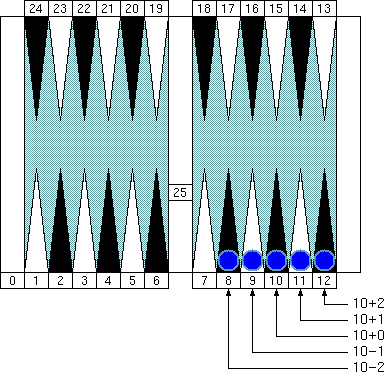
These points are all members of "Group 2."

---

"Group 3." Multiplying a group number ("3" in this case) by 5 gives us the "neutral number" 15 (= 3 × 5) that is the pip count of the checker of the group center.

---

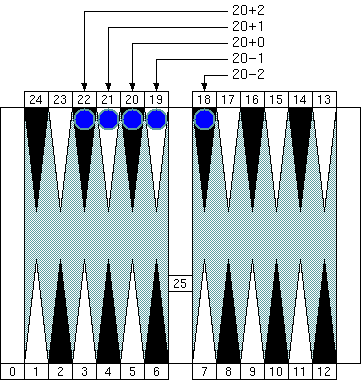
"Group 4." The neutral number of this group is 20 (= 4 × 5.)

---

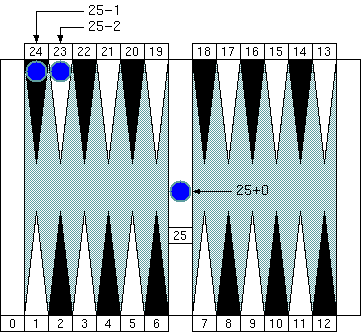
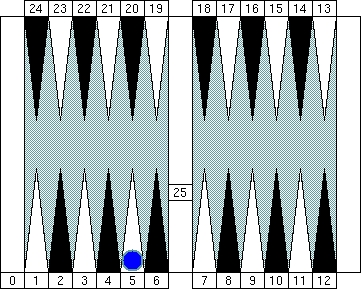
"Group 5." Note that the pip count of the bar is 25 and is also the neutral number of the group.

---

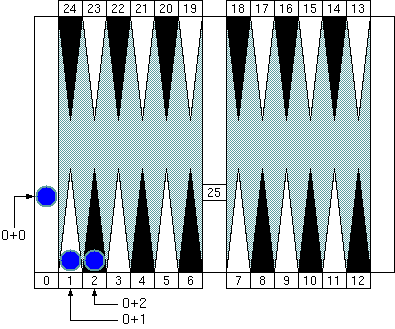
"Group 0 (zero)." Note that the pip count of the goal (the pocket) is 0 (zero) and is also the neutral number of the group.

---

We have seen that all points on the board can be separated into six groups from Group 0 to Group 5.

1.1.  Step 1: Group Counting

Here's an example position to explain my pip counting system.

By counting how many checkers in each group and multiplying the count by a group number,

0	checkers in the Group 0	0 × 0	=	0
9	checkers in the Group 1	1 × 9	=	9
1	checkers in the Group 2	2 × 1	=	2
2	checkers in the Group 3	3 × 2	=	6
2	checkers in the Group 4	4 × 2	=	8
1	checkers in the Group 5	5 × 1	=	5
			+)	30

We get 30 as a "Group counting" number.

1.2.  Step 2: Rough Counting

In order to get the "Rough counting" number, we multiply the "Group counting" number, 30 in this example, by 5. Multiplying 5 is not very easy task for most people, so why don't we just multiply the "Group counting" number by 10 instead of 5, and divide the result by 2. This way gives you the same result but should be much easier and faster.

(a) Multiply 30 by 10:  30 × 10 = 300

Just add one more 0 (zero) to the right of the group counting number. No need to think.

(b) Divide it by 2:  300 ÷ 2 = 150

We have got the "Rough counting" number, 150.

1.3.  Step 3: Adjustment

We have ignored those +2 to −2 errors for each point so far. In order to get the exact pip count of the example position, we will have to subtract or add the errors from or to the "Rough counting" number, 150. This adjustment process is not as hard as it first seems, although you may need some practice to get used to it. We will go through the process using the same example position.

The error numbers (−2, −1, 0, +1, +2) are shown above and below the board image.

---

Let's cancel all checkers placed on any neutral points whose errors are zero, because those points don't need any adjustment. In this example, we have two checkers on the 5 point and the other two on the 20 point.

Note that I circle checkers in a process with a bold pink line. I also check checkers already processed with a white line so that we can ignore those checkers in the further process.

---

The two checkers on the mid point (−2) and the two checkers on the bar point (+2) cancel out.

---

The one checker on the 3 point (−2) and two checkers of the four on the 6 point (1 × 2) cancel out.

---

The one checker on the 23 point (−2) and two checkers of the four on the 6 point (1 × 2) cancel out.

---

We have one more checker left on the 9 point (−1), which makes the adjustment −1.

The exact pip count of the position is:

150 (rough counting) −1 (adjustment) = 149

Continue on to:   Part 2: Techniques for Easier and Faster Counting

Sho Sengoku's Five Count Overview:   Summary of Sho's Pip Count, "Five-Count" Part 1:   Quick View: Introduction to "Five-Count" Part 2:   Techniques for Easier and Faster Counting Part 3:   Practice, Practice, Practice Part 4:   Even Faster! Part 4.1:   Common patterns for "10s" in group counting Part 4.2:   To get a "rough count" even faster Part 4.3:   Common cancellation patterns in an adjustment

 

See:  Other articles by Sho Sengoku

See:  Other articles on Pip Counting

Return to:  Backgammon Galore : Articles