General Form for Different Pip Counting Systems

Created by Sho Sengoku, 2003

There are good similarities among three different pip counting systems, Douglas Zare's "Half-Crossover Pipcount", Nack Ballard's "Naccel", and my system. Those three systems separate all 26 points of the board in a number of groups, assign a group center, and provide error numbers from the center point to locate any points in a group.

My system, the "Five-Count," is described here.

A detailed explanation for Douglas Zare's "Half-Crossover Pipcount" is available at this link

Nack Ballard's "Naccel" is explained in a GammOnLine article. Note that the "Naccel" shown in GammOnLine is slightly different from the one explained in Backgammon Today Sep. 2001 issue, but is the "bumped" one introduced in the magazine. The "Naccel" I referred in this page is the one with not bumped quads (the 6 point has 6 extra pips.)

To show "summation" operation, I use a "sigma" sign, Σ, as follows:

I also use these symbols:

xi	=	A pip count of a checker located any point. i = 1, 2, ... , 15
P	=	A total pip count.

Sho Sengoku's "Five-Count"

x_i = 5g_i + e_i
P = Σ(x_i) = 5Σg_i + Σe_i
where
g_i = 0, 1, 2, 3, 4, 5 (group)
e_i = −2, −1, 0, +1, +2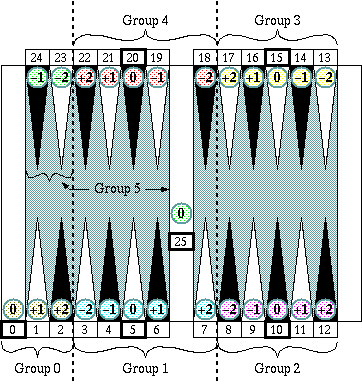

Douglas Zare's "Half-Crossover Pipcount"

x_i = 5 + 3h_i + e_i
P = Σ(x_i) = 75 + 3Σh_i + Σe_i
where
h_i = −2, −1, 0, 1, 2, 3, 4, 5, 6, 7 (half crossover)
e_i = −1, 0, +1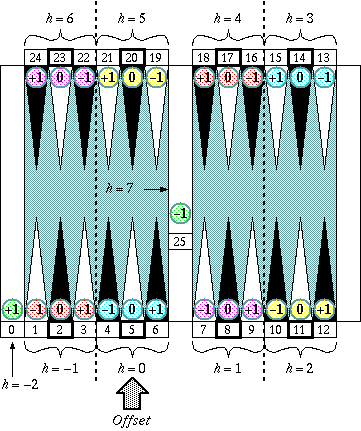

Note: the error number of the goal point (or the pocket) is +1 of h = −2.

Nack Ballard's "Naccel"

x_i = 6q_i + e_i
P = Σ(x_i) = 6Σq_i + Σe_i
where
q_i = 0, 1, 2, 3, 4 (quad)
e_i = +1, +2, +3, +4, +5, +6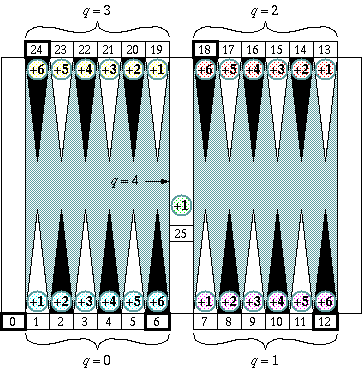

Since all e_i is positive (+) and Σe_i often becomes too big to handle for a human player, another breakdown in the Σe_i part is called for:

Σe_i = 6s + r
P = 6(Σq_i + s) + r
where
s = 0, 1, 2, ..., 15 (squad)
r = 0, 1, 2, ... (remains, usually r < 6)

Bumped Naccel

x_i = 6q_i + e_i
P = Σ(x_i) = 6Σq_i + Σe_i
where
q_i = 0, 1, 2, 3, 4 (quad)
e_i = 0, +1, +2, +3, +4, +5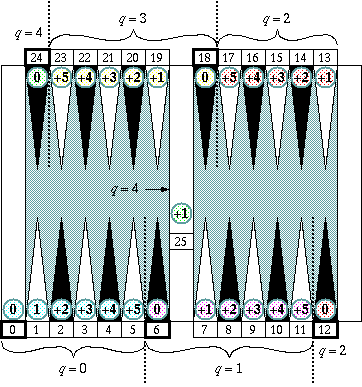

Home-Negative Naccel

x_i = 6 + 6q_i + e_i
P = Σ(x_i ) = 90 + 6Σq_i + Σe_i
where
q_i = −1, 0, 1, 2, 3
e_i = 0, +1, +2, +3, +4, +5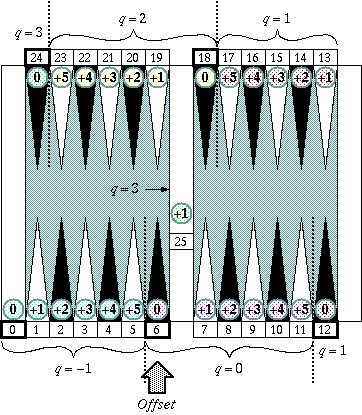

Home-Flop Naccel

x_i = 6 + 6q_i + e_i
P = Σ(x_i ) = 90 + 6Σq_i + Σe_i
where
q_i = 0, 1, 2, 3
e_i = 0, +1, +2, +3, +4, +5 (for q_i = 1, 2, 3)
e_i = −6, −5, ... , −1, 0, +1, ... , +5 (for q_i = 0)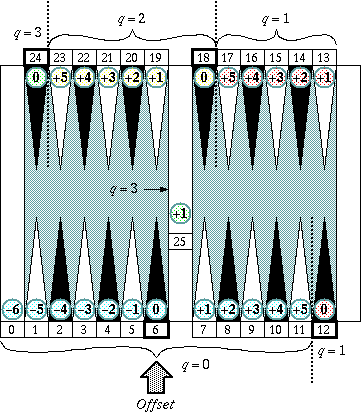

Note: the error number of the goal point (or the pocket) is −6.

General form

xi = F + Bgi + ei P = Σ(xi ) = 15F + BΣgi + Σei

Parameters

	B (base)	F (offset)	gi (group)	ei (error)
Five-Count	5	0	0, 1, 2, 3, 4, 5	−2, −1, 0, 1, 2
Half-Crossover	3	5	−2, −1, 0, 1, ... , 7	−1, 0, 1
Naccel	6	0	0, 1, 2, 3, 4	1, 2, 3, 4, 5, 6
Bumped Naccel	6	0	0, 1, 2, 3, 4	0, 1, 2, 3, 4, 5
HN Naccel	6	6	−1, 0, 1, 2, 3	0, 1, 2, 3, 4, 5,
HF Naccel	6	6	0 1, 2, 3	−6, −5, −4, ... , 4, 5 0, 1, 2, 3, 4, 5

See:  Other articles by Sho Sengoku

See:  Other articles on Pip Counting

Return to:  Backgammon Galore : Articles