
|
This article originally appeared in GammonVillage in 2000.
Thank you to Douglas Zare for his kind permission to reproduce it here.
|
|
Introduction
|
"And you do Addition?" the White Queen asked.
"What's one and one and one and one and one and one and one and one and one and one?"
|

| |
"I don't know," said Alice. "I lost count."
| |
—Lewis Carroll, Through the Looking Glass.
|
Perhaps I have gotten a bit rusty at mental arithmetic. I had
difficulty computing a pip count in backgammon, which I found a bit
embarrassing. It is a straightforward calculation, but the difficulty
was doing it accurately with no pencil and paper while an opponent
rattles the dice.
The approximate pip count is vital to correct backgammon play: "When ahead in
the race, race. When behind in the race, don't
race." Sometimes one needs more. The exact pip count is extremely
useful to guide one's doubling strategy in some situations. For
example, in a race of more than 70 pips, if you are on roll a good rule
of thumb is that if you lead by at least than 8% then you probably have a
correct double, and if your lead is at most 12% then your opponent
probably has a correct take. It arises in many other situations as
well.
Since the pip count is important, there have been a wide variety
of methods developed to compute it over the board. See Mark Driver's
article, "A
Beginner's Guide to Counting Pips" for one method and references
to more. There is some related discussion in the Pip Counting section
of the rec.games.backgammon archive.
As a kid, I did well on math competitions not by brute force
computation, but by a compilation of techniques. I would try to
recognize the easiest method for doing a problem. Sometimes this would
involve doing a different computation than normal just because it would
require less memory for intermediate results.
In the following, I'll
outline a method I use for doing pip counts which requires less mental
arithmetic and mental rearranging of checkers than any other I have
encountered. One doesn't even have to remember the numbers of the
points! It mainly involves counting, though it also uses adding 2-digit
numbers to 75 and multiplying 2-digit numbers by 3. As an added
benefit, along the way one gets an approximate pip count, which usually
suffices. I call this the half-crossover method.
|
|

|
The Half-Crossover Pip Count
|
Step 1: Count the half-crossovers to bear in.
Counting crossovers is easy, but not refined enough for a good approximate pip count. Instead, think of breaking each of the outer and inner boards in half, into triples: The first triple is 1-2-3, the next is 4-5-6, the third is 7-8-9, and the last is 22-23-24.
Let's assume that, rather than bearing off, your goal is to bear in. You want to bring your checkers to the 4-5-6 triple. Any checkers in the 4-5-6 triple get counted 0. The checkers in the 7-8-9 triple
would have to move forward one half-crossover. Those in the 10-11-12 triple have to move forward 2, those in the 19-20-21 triple would
have to move forward 5, and those in the 1-2-3 triple would have to
move backward 1.
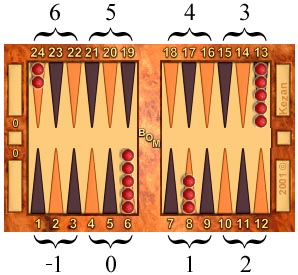
For example, from the starting position, you have 5 checkers already
there, 3 checkers that need to move forward 1 (subtotal 3), 5 checkers that need to move forward 3 half-crossovers (3 + 15 = 18),
and 2 checkers that need to move forward 6 half-crossovers (18 + 12 = 30).
If all you want to do is determine who is ahead, and by about how much,
then you can stop here. If someone is ahead by 2 half-crossovers, then
it is quite likely that they are actually ahead in the race. (This is
quite different from counting crossovers. Being ahead by one
crossover is a much weaker indicator of a racing lead.)
Step 2: Multiply this by 3, and add 75.
If all 15 checkers were on your 5, your pip count would be 15 × 5 = 75. There are 3 extra pips for each half-crossover to bring a checker into the 4-5-6 triple.
From the starting position, you have 30 half-crossovers to go, so you
add 3 × 30 = 90 to 75 to get 165 as your approximate
pip count.
Step 3: Fine tune.
Subtract 1 for each checker on the front of its triple. Add 1 for each checker on the back of its triple.
What we did in the previous step was to assume that every checker was
in the middle of its triple, that every checker in the 4-5-6 triple
was actually on the 5. A checker on your 6 is one step further
away, so add one for each checker which needs to be pushed forward to
the middle of its triple. Similarly, a checker on your 4 is one step
closer than we counted, so subtract one for each checker that needs to
be pushed back to the center of its triple.
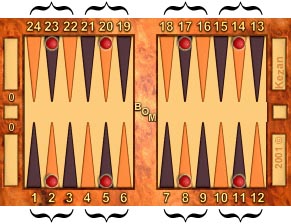 |
|
These points are the centers of triples, and count 0.
|
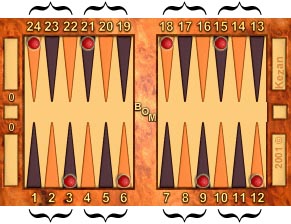 |
|
These are the backs of triples for red, and count +1.
|
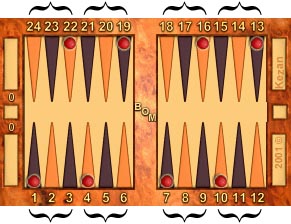 |
|
These are the fronts of triples for red, and count −1.
|
In the starting position, you have 5 checkers on your 6 that need to be
pushed forward minus 5 checkers on your 13 that need to be pushed back
plus 2 checkers on your 24 that need to be pushed
forward. 5 − 5 + 2 = 2, so
one needs to adjust the approximation computed in Step 2 by adding
2: 165 + 2 = 167, the exact pip count.
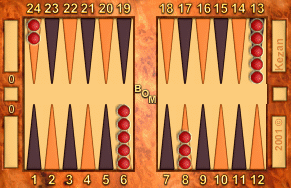
Feel free to cancel +1's and −1's that you can pair up. Since the 6 point and midpoint cancel, the modifications to the approximate pip count are a bit smaller than one would expect by random chance. (Also, it is quite reasonable to count on your fingers. If you keep them under the table other people won't notice.) The net modification (between red and white) is usually less than 5 pips.
|
|

|
Refinement and Practice
|
|
Rather than Step 1, one could also count the crossovers, then subtract
one half for each checker in the front half of its board. One would
multiply this number by 6 in Step 2.
I find Step 1 to be the hardest part, though with practice I can still
do it in under 5 seconds per side. If you don't like multiplying, it is fast
enough to count the half-crossovers for each checker individually! For
example, consider the following position:
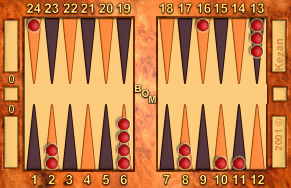 |
|
Position 1
|
Rather than (-1 × 2) + (1 × 2) + (2 × 2) + (3 × 3) + (4 × 1) + (6 × 1) one could count (−1, −2), (−1, 0), (1-2, 3-4), (5-6-7, 8-9-10, 11-12-13), (14-15-16-17), (18-19-20-21-22-23) for a total of 23 half-crossovers to bear in.
Checkers on the Bar and Borne Off
Note that I haven't dealt with checkers on the bar or already borne
off. One could easily incorporate them by saying that a checker on the
bar needs to be pushed forward 7 half-crossovers (then subtract 1 pip
in step 3) and a checker that is off has to be pushed back 2
half-crossovers (then add one pip). One could also just add 20 pips
for each checker on the bar and subtract 5 for each one already off.
However,
usually when one has multiple checkers on the bar the pip count is not as
vital, and when one is bearing off one should make the target triple be
1-2-3 rather than 4-5-6, so add 30
pips rather than 75 in step 2, and subtract 2 pips at the end for
each checker that is off.
Examples
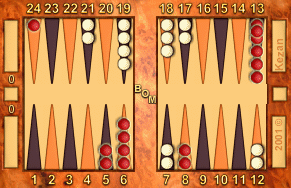 |
|
Position 2
|
For red: 26 HC's to go, for an estimate of 75 + 78 = 153, modified +1, 154.
For white: 19 HC's to go, for an estimate of 75 + 57 = 132, modified −1, 131.
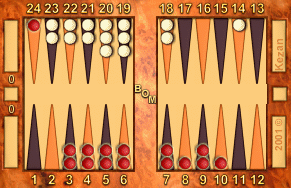 |
|
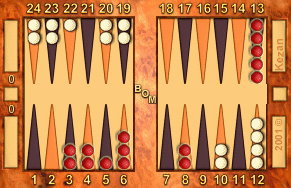
Position 3
|
For red: 11 HC's to go, 75 + 33 = 108, modified +2, 110.
For white: 0 HC's to go, 75 + 0 = 75, modified +1, 76.
 |
|
Position 4
|
For red: 15 HC's to go, 75 + 45=120, modified −2, 118.
For white: 13 HC's to go, 75 + 39 = 114, modified −1,
113.
As with any pipcount method, it is useful to practice. I hope you will find
that this method takes substantially less time to practice, though. You might
find it worthwhile to combine a counting method with a simple way of
representing 2-digit numbers on your hands, so that you can ignore the first
side's pip count as you do the second. (Thanks to multiple messages in
rec.games.backgammon and to the bulletin board of Gammonline for this
suggestion.)
My chamber-music friends will be delighted to know that I have finally learned
to count.
|
|
© 2000 by Douglas Zare.
Douglas Zare is a mathematician and backgammon theorist. He writes a monthly column at GammonVillage on the theoretical aspects of backgammon. His web site is douglaszare.com.


See also: Other articles on pip counting.
See also: Other articles by Douglas Zare.
Return to: Backgammon Galore
|





![]()









