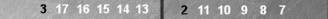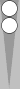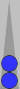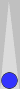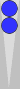This is Part 4 of the Naccel 2 series. For this post, Lucky Jim submitted two positions.
You know about reflections on the near side (see poofs). Cancellations around
S0 (trad 6pt) count zero, which means there are a lot of checkers you
don't have to count at all.
There are also reflections on the far
side. Because they reflect around S2 (opponent's bar point) instead of S0,
they count 2 per checker—that is, count the number of checkers you
see and double it.
With the midpoint featured, this is the most commonly arising far-side reflection:
Doubling the number of checkers, 4, gives us a count of 8. (If these were blots instead of points, the count would be only twice 2 = 4.)
Let's apply that knowledge to the Blue side of Jim's first position:
Blue's checkers on the near side reflect around the 0pt and therefore
cancel out except for the 2pt checker (which counts 2 pips). So ...
8 (reflection), plus 9 for S3, plus 2 pips for the blot, gives a count of 17(2).
[Jim
and Ian counted similarly, except they didn't yet know about far-side
reflection. Instead, they shifted to S3 and S1, which is fine but it
adds a step of visualization.]
White's
count is even easier (as Jim and Ian found as well), so it's hardly
worth a new diagram, but I'll spend one anyway so that the point
numbering is from White's point of view.
White's entire near side goes poof (reflection/cancellation around the 0pt), so the entire count is 3(3).
The
midpoint is nice for leftover counts because it's trivial to multiply
1(1) for each checker, and if it has as many as six checkers it just
counts 7. (Naturally—a six-stack on the 7pt = 7.)
In short, the count is 17(2) to 3(3), a difference of about 14 supes
(super-pips).
[Round supes (which can be thought of as crossovers) are
a good way to assess Blue's timing. As 12 of the 14 supes are accounted
for in bringing home the vital-to-keep anchors, that only leaves 2
spare supes, which are roughly offset when White's 6s then 5s are
killed bearing in later. And the S3 spare might not escape and get its
3 supes. Yikes, looks like a monster pass.]
If
you are unclear as to why Blue's near side counts only 2 pips and
White's near side is a giant poof that doesn't need to be counted at
all, review the fourth and fifth diagrams in Part 1.
Below
is Jim's second position. There are many ways to count Blue (I'll show
you my count later) but I'll give you a way that works well with what
you know so far.
For Blue, try this easy mental shift:
Now, here's the trick that you need: Conjure a new checker on the 0pt.
Remember, the 0pt is not only a black hole but also a white hole: even
when the 0pt looks vacant, phantom checkers always exist there for your
convenience. Now, lift that conjured 0pt checker onto the −1pt, which
is a 1 pip adjustment.
So,
your count: Four on S3 counts 12, six-sym (around the −3pt) is −3, the
engineered six-stack is −1, and add the 1-pip lift needed to get that
stack. That's a net of 8(1).
Now let's count White. Her position again is ...
Try this mental shift (2 pips forward, 2 pips back):
The stack is −3, the six-sym (three-prime) is −1, and the three spares
on the −1pt are −3 pips. Total of −4(−3). In case you want to convert,
−4 × 6 − 3 + 90 = 63.
Do
you see a similarity with what we did in Blue's inner board and in
White's inner board? Six-stacks and six-syms (which are often
three-primes) are powerful weapons.
When both
Blue and White checkers are home, cluster-counting is relatively at its
best. With only one quadrant to count, Naccel's edge disappears. But if
you want to become lightning fast, it pays to practice counting all
positions with Naccel (instead of lazily falling back), even though at
first it may be slow and even confusing in certain situations. That's
to be expected—you're still tying your skate laces at this point.
Finally, I promised to show you the way I counted Blue (noting that the
alternative method suggested above is perfectly legit). To understand
my count, you'll need two key pieces of information.
First, let's review the mirror, introduced in Part 3. Below is another example:
For a regular mirror, the near-side point is (as you can see) a pip
closer to the bear-off tray (than the far-side point would be if it
were dropped straight down). The number of checkers = 4, and thus the
count = 4.
For
advanced anchors (or blots), you can often use regular mirrors to
offset checkers in the home board. But for deep anchors, you will tend
to use "zag-mirrors" (or "zags" for short).
Starting
with the mirrored point shown above (count of 4), if you zag (move back)
either point 3 pips, you increase the count by 6 pips or 1
supe, to a count of 5, and you have yourself a zag mirror.
If it is the far-side point that is zagged, we get the zag mirror shown below.
Whereas with regular mirrors, the near-side point is 1 pip closer to
the bearoff tray; with zag mirrors, the near-side point is 2 pips further away.
As stated, zag-mirrors count 5. The occupied points are opposite colors, which helps remind you that the count is odd.
Now for the second part of the explanation:
A triplet (three-stack), which was introduced in Part 3, is a basic squad (i.e., a group of checkers within a quadrant field). An example is shown below.
As was explained in Part 3, you count a triplet by dividing the number
of the point on which it resides by 2. This triplet is on the −2pt, so
the count is −1.
The
triplet has a variant squad, which can be obtained by moving two of the
checkers 1 pip towards the nearest Super, and the third checker 2 pips
in the other direction, to compensate. It looks like this:
This squad is called a "wedge" (it is shaped like a door wedge). To
count a wedge, take the point number that is in between the blot and
point but closer to the latter (or just shift to it, thereby reenacting
a triplet on the appropriate point, if you need the visual help), and
divide it by 2.
Here, the in-between point is the −2pt. Dividing by 2 gives you this wedge's count of −1.
You can also double the height of the wedge which gives you a "double wedge," and this also-commonly seen formation counts the same
as the in-between point number (e.g., if you double the height of the
wedge shown above, the count is −2). Both the wedge and the double
wedge can be great counting tools.
Now that you know what a zag (zag mirror) and a wedge are, I'll show you how I counted Blue in Jim's
position, repeated below.
To count Blue, all I did was to move one pip forward, from the 0pt to the −1pt, and sum the count of two formations:
That's 10 for the double zag, −2 for the double wedge, plus the 1-pip lift: my count is 8(1).
The checker left on the 0pt, is, as usual, invisible.
Go on to Part 5, or read more below.
| 




![]()