|
Cluster Counting
|
Jack Kissane
November 1992
|
This article originally appeared in the November 1992 issue of Chicago Point.
Thank you to Jack Kissane and Bill Davis for their kind permission to reproduce it here.
|
|
|
Introduction
|
 |
Jack Kissane, backgammon master from Albany, New York, is known in many
chouette circles as the fastest pip counter in the world. In a June 1989 Chicago Point interview, Kissane claimed
that he can count almost any backgammon position within five seconds.
For the first time anywhere, Jack Kissane shares his counting techniques with
the backgammon community. Enjoy! |
Pip counting. How do you view it? An annoyance? A necessity? Just part of the
game? Some backgammon players can't or won't be bothered doing a pip count.
Others use the count as a crutch, basing far too many checker moves on it.
After
a hard day of match play or during an all-night chouette, pip counting can be
sheer torture, draining our limited supply of "thinking" energy. However, once
or twice a game, knowing the count is critical for making the right checker play
or, more importantly, the correct cube decision.
Over the years, I have developed a system of pip counting that significantly
reduces the amount of time needed to count a position. I call it Cluster
Counting. Hopefully, this fairly simple system will help you minimize the
drudgery of pip counting and thus increase your enjoyment of the game.
Basically, Cluster Counting involves the mental shifting of checkers to form
patterns of reference positions (RP's) whose pip totals end in zero (with
two notable exceptions) for quick, easy and accurate addition. Here are my seven
basic reference positions:
|
|

|
Reference Positions
|
|
Multiply the midpoint of any 5-prime by 10 and you have just counted a cluster of ten checkers.
 |
|
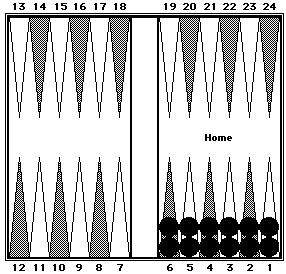
This position shows a 5-prime from the 4-point to the 8-point.
The 6-point is the midpoint and the count for these ten checkers = 60 pips (6 × 10.) This is so because 5's and 7's average out to 6's, and 4's and 8's also average out to 6's.
Black = 60.
|
 |
|
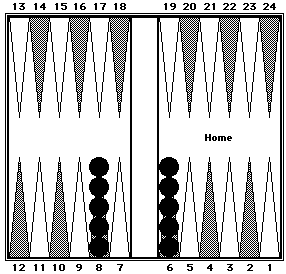
This is just a 5-prime around the 4-point plus two checkers on the ace point.
Black = 42.
|
 |
|
Five checkers each on the 6- and 8-points.
Black = 70.
|
 |
|
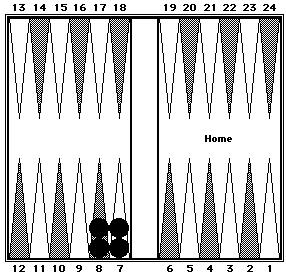
Two checkers each on the 7- and 8-points.
Black = 30.
|
 |
|
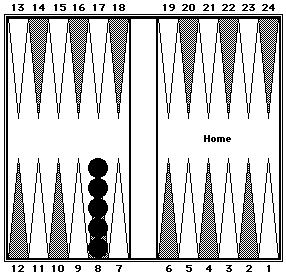
Five checkers on the 8-point.
Black = 40.
|
 |
|
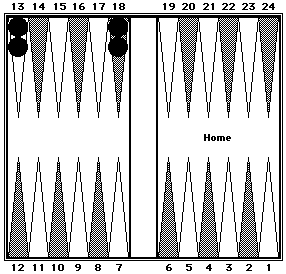
Two checkers each on the midpoint and opponent's bar point.
Black = 62.
|
 |
|
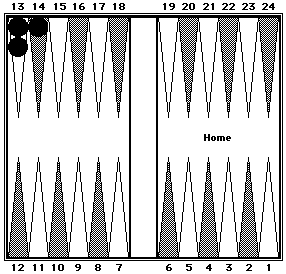
Two checkers on the midpoint and one on the 14 point.
Black = 40.
|
These seven reference positions combined with key points and mirrors are the backbone of Cluster Counting.
|
|

|
Key Points
|
The two key points most often used are the 5-point and the 20-point (opponent's 5-point). The 10-, 13- and 15-points are also quite valuable.
Using 5-Point as Key Point
 |
|
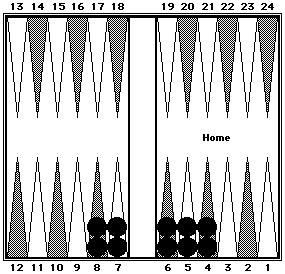
This position shows two examples of counting a cluster of eight checkers all at once as if they were eight 5's = 40.
Black = 40. White = 40.
|
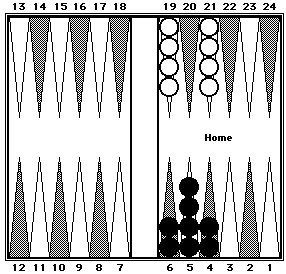
Using 20-Point as Key Point
The 20-point (opponent's 5-point) is the most useful key point. All checkers in your opponent's home board should be counted as 20 plus the pips required to get to the 20-point.
 |
|
Black's count is 108 which can be visualized as five 20's + 4 (two each from the 22-point to the 20-point) + 4 (one from 24-point to 20 point).
White's count is 89, visualized as four 20's + 4 + 5 (for the checker on the bar).
Black = 108. White = 89.
|
|
|

|
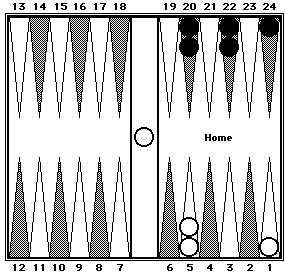
Mirrors
|
|
Mirrors are another important counting tool. Any point on the board plus its mirror-opposite point equals 25. For example, the 5-point + 20-point, the 1-point + 24-point, and the 12-point + 13-point all total 25 pips. It follows that any cluster of 4 checkers in mirror positions total 50.
 |
|
Black: (20 + 5 = 25) × 2 = 50.
White: (13 + 12 = 25) × 2 = 50.
Black = 50. White = 50.
|
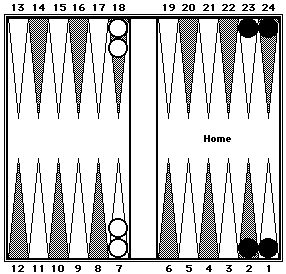 |
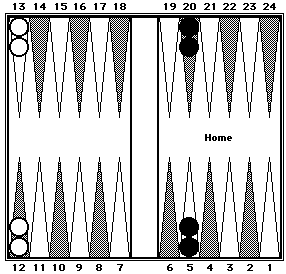
|
Black: (23 + 2 = 25) + (24 + 1 = 25) = 50 .
White: (18 + 7 = 25) × 2 = 50.
Black = 50. White = 50.
|
|
|

|
Mental Shifting
|
Ok! It would be nice if every time you needed a pip count, the board would consist of clusters as previously described. Unfortunately, that doesn't happen. Fortunately, these easy-to-count clusters are relatively simple to form by mentally moving the checkers where you want them.
One-Way Mental Shift
One-way mental shifting involves moving the checkers forward to key points or reference positions and then adding the forward movement to the value of the key points or reference positions.
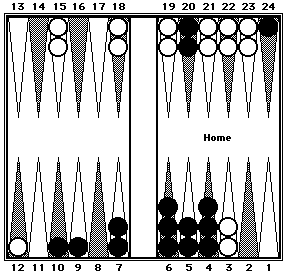 |
|
Black can be easily counted in three clusters: 40 (eight 5's) + 33
(RP4 + 3 pips) + 64 (three 20's + 4) = 137.
Divide White's checkers into three clusters: 44 (5-prime + 4 pips forward, 2 each from the 7-point to the 5-point) + 33 (three 10's + 3 pips from 13 to 10) + 44 (two 20's + 4) = 121.
Black = 137. White = 121.
|
Note that two of White's checkers were shifted to White's 5-point which is occupied by Black's checkers. When shifting one player's checkers, the other player's checker position can be ignored.
Two-Way Mental Shift
Two-way mental shifting differs from one-way mental shifting in that checkers are shifted either forward or backward to key points or reference positions and then compensating shifts are made in the opposite direction on the same side of the board, or in the same direction on opposite sides of the board.
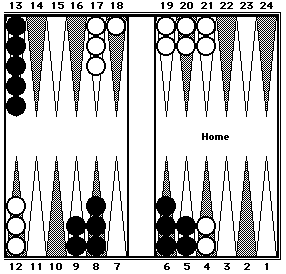 |
|
Black's spare checkers on the 6- and 8- points are on the same side of the board. By shifting them one pip in opposite directions to the 7-point, a 5-prime is formed. Black's position can easily be counted in two clusters: 70 (5-prime) + 65 (five 13's) = 135.
White's spare checkers on the 8- and 13-points are on opposite sides of the board. By shifting them in the same direction, in this case left-to-right, a 5-prime is formed (RP1) and RP7 is also formed. White's position can then be counted in three clusters: 60 + 40 + 42 (two 20's + 2) = 142.
Black = 135. White = 142.
|
It should be noted that there are often several cluster counting choices available. For instance, in Black's position above, instead of forming a 5-prime, you could have shifted the two 9-point checkers to the 8-point and compensated by shifting the two 5-point checkers to the 6-point to form RP3. This cluster is also 70 pips.
|
|

|
Your Turn
|
Let's try counting some positions. Original positions and adjusted positions (after shifting) are shown but not described. Can you spot the shifts? If not, set them up on your backgammon board and they will become clear.
Example 1
|
Before shifting
| |
After two-way mental shifting
|
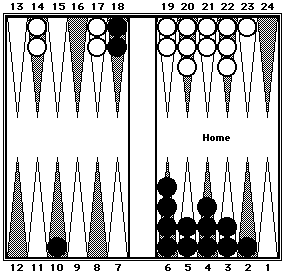 |
|
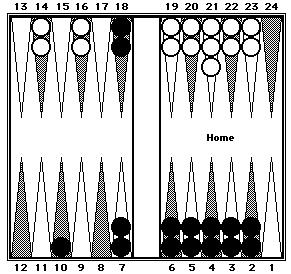 |
Black can be counted in three clusters: 40 (5-prime from the 6-point to the 2-point) + 50 (mirrors on the 7-point and the 18-point) + 10.
White can be counted in two clusters: 44 (5-prime + 4) + 40 (four 10's).
Black = 100. White = 84.
Example 2
|
Before shifting
| |
Black's position after shifting
|
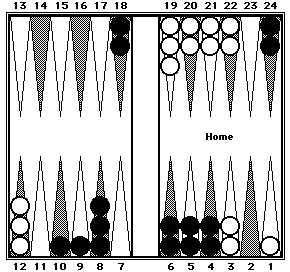 |
|
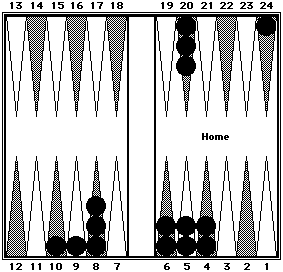 |
Black can be counted in three clusters: 30 (six 5's) + 43 (RP5—five 8's + 3) + 84 (four 20's + 4).
|
Before shifting
| |
White's position after shifting
|
 |
|
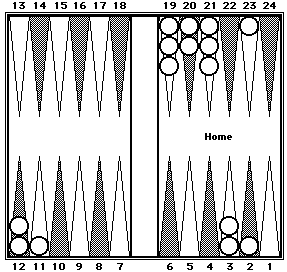 |
White can be counted in three clusters: 42 (eight 5's + 2) + 40 (RP7) + 67 (three 20's + 7).
Black = 157. White = 149.
Example 3
|
Before shifting
| |
After shifting
|
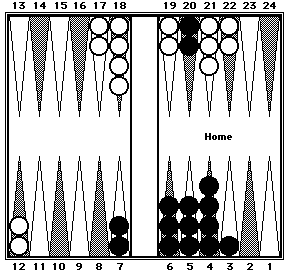 |
|
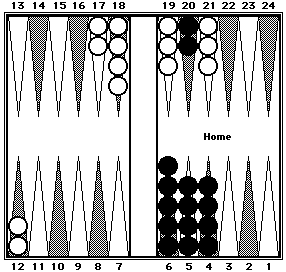 |
Black can be counted in two clusters: 66 (twelve 5's + 6) + 40 (two 20's).
White can be counted in two clusters: 30 (six 5's) + 70 (RP4 × 2 + 10 for two checkers moved from the 13-point to the 8-point).
Note that in the shifted position White has only 14 checkers. The two checkers originally on the 3-point were shifted in different directions—one checker to the 6-point and the other checker off the board.
Black = 106. White = 100.
Example 4
As previously noted, with Cluster Counting there is almost always more than one correct way to count a position. You should use whichever cluster formations you can quickly visualize. For example:
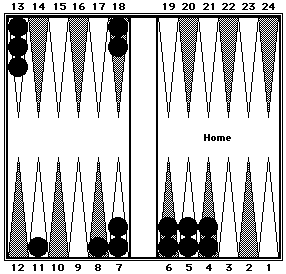
With a minimum of shifting, Black's position can be quickly counted in several different ways:
- 63 (5-prime + 3) + 75 (five 13's + 10 by shifting two checkers from the 18-point to the 13-point);
- 63 (5-prime + 3) + 62 (RP6) + 13 (spare checker on the 13-point);
- 50 (mirrors on the 12- and 13-points) + 50 (mirrors on the 7- and 18-points) + 30 (six 5's) + 8 (checker on the 8-point).
Black = 138.
Well, that's the system. Certainly my list of seven reference positions is by no means inclusive. You probably already know or will discover other positions that can be added to the list.
Will mastering the Cluster Counting technique improve your game, or at least make one tedious aspect of backgammon more enjoyable? Count on it!
|
|

Kevin Bastian created the graphics for this page. Kate McCollough created the original HTML.

See also: Other articles on pip counting.
Return to: Backgammon Galore
|







![]()





















