Introduction
Suppose a single elimination tournament has a number of entrants which is a power of two times a whole number which is not a power of two that would be a convenient number of places to pay. For example 48 players playing down to either 3 or 6 players, or 40 players playing down to 5, or 56 players playing down to 7.
48 = 24 × 3 or 23 × 6
40 = 23 × 5
56 = 23 × 7
|
The tournament could initially then be drawn up without byes. The field could play down to the prize winners and then a fresh draw of those remaining could be done.
If nothing fancy is done clearly there is substantial equity in drawing a bye at that point. To even out the luck of the draw the players who do not receive byes could be compensated.
The Method
There have been some unnecessarily complicated ways of this being handled but the following method is simple to implement, simple to explain, and simple to handle regarding payouts.
|
Let n denote the number of players. First give 1/(2n) of the prize pool to each player who did not get a bye. The remaining portion of the prize pool will then be played for.
|
A formal proof that this technique gives each player the same equity is given at the end. Here are a few examples that show the basic idea of how it works and why it is equitable:
- If 5 players remain then 3 players have a bye into the round of 4 and 2 play an extra round. One tenth of the prize money is removed from the prize pool and given to the 2 playing the extra round, leaving 4/5 of the original prize pool to be played for. Once that is done the tournament just proceeds naturally. Supposing a $10,000 prize pool, $1,000 is given to each of those two players and then $8,000 remains. However this is split up would be equitous but a common division might be $4,000 to the winner, $2,000 to the finalist, and $1,000 to the two semifinalists. If a player who did not receive a bye initially wins, that prize it is in addition to the $1,000 given originally.
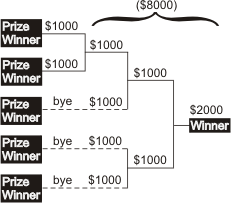
Why is this equitable? Each player should have equity of 1/5 of the original prize pool. The three players with a bye have equity of 1/4 of the prize pool that remains after the non-bye players are compensated giving here (1/4)(4/5) = 1/5 of the original prize pool as it should be.
By symmetry and the fact that the equities add to 1, the other two players must also have 1/5th each.
An alternative way to see it is that they each have 1/10 + (1/8)(4/5) = 1/10 + 1/10 = 1/5.
- If 7 players remain then 1 player has a bye into the round of 4 and 6 play an extra round. Each of the non-bye players gets 1/14 of the prize pool Leaving 8/14 = 4/7 to be played for. Then as before the tournament proceeds. For example, with a prize fund of $1,400, the 6 non-bye players get $100 each leaving $800 in the prize pool. It could be split up as $400, $200, $100, $100. Note here that the non-bye players have equity of (1/4) (4/7) = 1/7 as should be and again, by symmetry and adding to one, that the equity of the non-bye players must also be 1/7.
- Suppose we have a large tournament of 96 players. Depending on how many places are to be paid they could play down to 3, 6, or 12 (or even a larger number). Let's say that 12 will cash.
We will have 4 players with a bye into the round of 8 and 8 players having to play an extra round. Those 8 players each get 1/24 of the prize pool leaving 16/24= 2/3 to be played for. Note here that the bye players have equity of (1/8)(2/3) = 1/12 as it should be and again the non-bye players also have 1/12.
Directors sometimes are hesitant to expand an elimination tournament past a natural power of 2. But with this technique the following number of players become "nice".
Powers of 2 of course remain nice: 4, 8, 16, 32, 64, ...
Playing down to 3 (or 6): 6, 12, 24, 48, 96, ...
Playing down to 5: 5, 10, 20, 40, 80, ...
Playing down to 7: 14, 28, 56, ...
A few warnings are in order. First of all this technique does not directly concern the issue of a sidepool. It should be made clear in advance how that will be handled. Secondly if an ABT tournament uses this technique it should be made clear how the points are to be distributed. They could mirror the percentages of the prize pool or just reflect the final standings. The first method may seem a little more fair but note that it gives a chance for the winner to receive a very large share of the points if it is an anti-bye player.
Appendix
Theorem: The technique described earlier results in each player having the same equity after the draw, namely 1/n of the original prize pool.
Proof: We have that n, the number of players, is not a power a 2. Let p be the greatest whole power of 2 so that p < n. Players receiving a bye have equity of 1/p of the prize pool that remains after the non-bye players have been compensated. The number of players not receiving a bye is 2(n-p). This gives a total removed from the prize pool of 1(2n) × 2(n − p) = (n − p)/n. Thus, p/n remains in the prize pool.
The equity of the players receiving a bye is thus (1/p) × (p/n) = 1/n. By symmetry the equity of each of the non-bye players is equal. Further, since the total equity must be 1 the equity for each of those players must also be 1/n.
|



![]()

