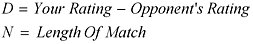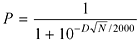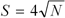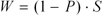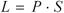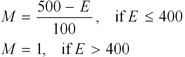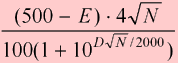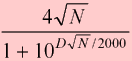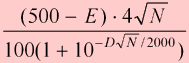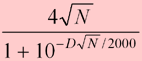
|
Ratings
|
Introduction
|
|
Everyone starts with a rating of 1500. When you win a match, your rating goes up. When you lose a match, your rating goes down. Over time, your rating will tell you, roughly, how strong a player you are.
|
|
|
There is no international rating system as there is in chess. The easiest way to get a rating is to play one of the many online play sites. Most sites have their own built-in ratings sytem. Just play matches and you will get a rating.
On some sites, you have to choose whether you want your matches rated or not. On others, you have to be a paying member to get a rating.
|
|
|
You can use your rating to see how well you play compared with other players on the same site. The following chart gives a rough idea of how you might interpret your rating.
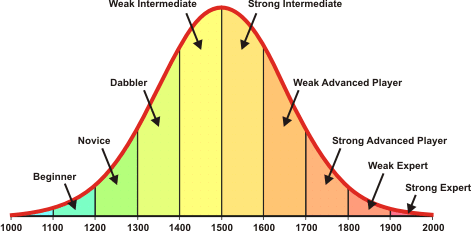
It is more difficult to compare your rating with players from other sites. Not all sites use the same rating formula, and the overall strength of players on different sites varies.
|
|
- Whether you win or lose. If you win a match, your rating goes up; if you lose, your rating goes down.
- The length of the match. Winning a long match changes your rating more than winning a short match. The reason is that the outcome of a longer match is more likely due to skill and less likely the result of luck.
- Rating difference. Winning a match against a higher rated player increases your rating more than winning against a lower rated player.
- Number of matches played. New players will see their rating change in larger steps during an initial ramp-up period.
|
|
- How much you win or lose the match by.
It doesn't matter if you win a match by one point or ten points; a win is a win. For example, in a 3-point match, winning 3-2 is the same as winning 12-0. You don't receive additional rating points for a large margin of victory.
|
|
 In the late 1980's, Kent Goulding sought to establish a ratings system for backgammon. He asked his friend, Larry Kaufman, who was familiar with the workings of the chess system, to devise an appropriate system. Kaufman took the chess system, which was devised by Arpad Elo in 1960, and modified it to make it more suitable for backgammon. He described his proposal in a 1991 article in Inside Backgammon.
Around the same time, Andreas Schneider was developing FIBS. Schneider came upon Kaufman's article and decided this was exactly what was needed for his new play site. The ratings system was a hit. Players now had an easy way to track their performance against others, and this added greatly to the fun. Today, most backgammon play sites use a rating system based on the Elo/Kaufman/FIBS model.
|
|
|
Rating Formula
|
|
Let D be the difference between your rating and your opponent's rating, and let N be the length of match you are playing.
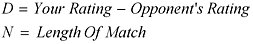
Then the rating formula predicts your probability of winning is:
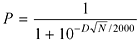
Here's how this works out for typical match lengths at several rating differences:
Probability of Winning
Rating
Diff (D) | Match Length (N) |
| 1 | 3 | 5 | 7 | 9 | 11 | 15 | 25 |
| -500 | .360 | .270 | .216 | .179 | .151 | .129 | .097 | .053 |
| -400 | .387 | .311 | .263 | .228 | .201 | .178 | .144 | .091 |
| -300 | .415 | .355 | .316 | .286 | .262 | .241 | .208 | .151 |
| -200 | .443 | .402 | .374 | .352 | .334 | .318 | .291 | .240 |
| -100 | .471 | .450 | .436 | .424 | .415 | .406 | .390 | .360 |
| 0 | .500 | .500 | .500 | .500 | .500 | .500 | .500 | .500 |
| 100 | .529 | .550 | .564 | .576 | .585 | .594 | .610 | .640 |
| 200 | .557 | .598 | .626 | .648 | .666 | .682 | .709 | .760 |
| 300 | .585 | .645 | .684 | .714 | .738 | .759 | .792 | .849 |
| 400 | .613 | .689 | .737 | .772 | .799 | .822 | .856 | .909 |
| 500 | .640 | .730 | .784 | .821 | .849 | .871 | .903 | .947 |
For example, if you are rated 200 points higher than your opponent and you play a 9-point match, then your chance of winning the match is 66.6%.
|
|
|
The number of rating points at stake is the difference between what your rating will be if you win a match and what it will be if you lose. The only thing that affects points-at-stake is the length of the match.
If N is the length of the match you are playing, then the points at stake are
|
|
|
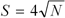
The number of points you receive when you win a match depends on P (your probability of winning, defined here) and S (the number of points at stake, defined here). The following formula tells how many points you win:
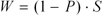
Basically, the formula says, "the greater your chances of winning, the the fewer points you gain when you win." Here are some examples:
Points Added to Your Rating When You Win
Rating
Diff (D) | Match Length (N) |
| 1 | 3 | 5 | 7 | 9 | 11 | 15 | 25 |
| -500 | 2.56 | 5.06 | 7.01 | 8.69 | 10.19 | 11.55 | 13.99 | 18.94 |
| -400 | 2.45 | 4.78 | 6.59 | 8.17 | 9.59 | 10.90 | 13.26 | 18.18 |
| -300 | 2.34 | 4.47 | 6.12 | 7.55 | 8.86 | 10.07 | 12.27 | 16.98 |
| -200 | 2.23 | 4.15 | 5.60 | 6.86 | 7.99 | 9.05 | 10.99 | 15.19 |
| -100 | 2.12 | 3.81 | 5.04 | 6.09 | 7.03 | 7.88 | 9.44 | 12.80 |
| 0 | 2.00 | 3.46 | 4.47 | 5.29 | 6.00 | 6.63 | 7.75 | 10.00 |
| 100 | 1.88 | 3.12 | 3.90 | 4.49 | 4.97 | 5.38 | 6.05 | 7.20 |
| 200 | 1.77 | 2.78 | 3.35 | 3.73 | 4.01 | 4.22 | 4.50 | 4.81 |
| 300 | 1.66 | 2.46 | 2.83 | 3.03 | 3.14 | 3.20 | 3.22 | 3.02 |
| 400 | 1.55 | 2.15 | 2.35 | 2.42 | 2.41 | 2.37 | 2.23 | 1.82 |
| 500 | 1.44 | 1.87 | 1.93 | 1.89 | 1.81 | 1.71 | 1.50 | 1.06 |
|
|
|
The number of points taken from your rating when you lose a match depends on P (your probability of winning, defined here) and S (the number of points at stake, defined here). The following formula tells how many points you lose:
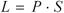
Basically, the formula says, "the greater your chances of winning, the more points you lose when when you lose." Here are some examples:
Points Deducted from Your Rating When You Lose
Rating
Diff (D) | Match Length (N) |
| 1 | 3 | 5 | 7 | 9 | 11 | 15 | 25 |
| -500 | 1.44 | 1.87 | 1.93 | 1.89 | 1.81 | 1.71 | 1.50 | 1.06 |
| -400 | 1.55 | 2.15 | 2.35 | 2.42 | 2.41 | 2.37 | 2.23 | 1.82 |
| -300 | 1.66 | 2.46 | 2.83 | 3.03 | 3.14 | 3.20 | 3.22 | 3.02 |
| -200 | 1.77 | 2.78 | 3.35 | 3.73 | 4.01 | 4.22 | 4.50 | 4.81 |
| -100 | 1.88 | 3.12 | 3.90 | 4.49 | 4.97 | 5.38 | 6.05 | 7.20 |
| 0 | 2.00 | 3.46 | 4.47 | 5.29 | 6.00 | 6.63 | 7.75 | 10.00 |
| 100 | 2.12 | 3.81 | 5.04 | 6.09 | 7.03 | 7.88 | 9.44 | 12.80 |
| 200 | 2.23 | 4.15 | 5.60 | 6.86 | 7.99 | 9.05 | 10.99 | 15.19 |
| 300 | 2.34 | 4.47 | 6.12 | 7.55 | 8.86 | 10.07 | 12.27 | 16.98 |
| 400 | 2.45 | 4.78 | 6.59 | 8.17 | 9.59 | 10.90 | 13.26 | 18.18 |
| 500 | 2.56 | 5.06 | 7.01 | 8.69 | 10.19 | 11.55 | 13.99 | 18.94 |
|
|
|
Let’s say you play a 3-point match. The points at stake in a three-point match is 6.9. That is the square root of 3, multiplied by 4. This means that if you win the match, your rating will be 6.9 points higher than if you lose.
Now suppose you play someone rated 300 points lower than you. The rating formula says you have a 65 percent chance of winning this match. If you win, your rating will go up 35 percent of 6.9 points (up 2.4 points); if you lose, your rating will go down 65 percent of 6.9 points (down 4.5 points).
Note, if the formula is correct and you really do win 65 percent of the time, you'll break even in the long run. If the formula underestimates your chances and you actually win 75 percent of the time, your rating will go up over time. If the formula overestimates your chances and you win only 55 percent of the time, your rating will go down over time.
|
|
|
The ramp up is a feature of the rating formula designed to accelerate rating changes for new players. Because everyone starts with an arbitrary rating of 1500, ratings of new players can be off by a lot. During an initial ramp-up period, rating changes are magnified to help new players achieve their correct rating faster.
On FIBS, rating changes are ramped until you have accumulated 400 experience points. Experience is the total length of rated matches you have completed. For example, if you have completed three 5-point matches, your experience is 15.
If your experience is E, then the amount by which your rating changes are magnified is:
|
|
|
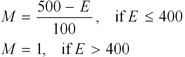
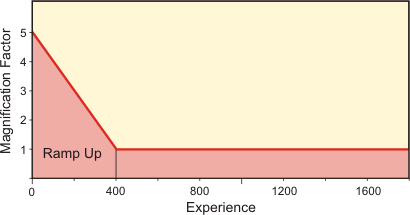
Here is an example. Bert and Ernie play a series of one-point matches. They both start with a rating of 1500. Bert is a better player and wins 2/3 of the matches they play, so Bert's rating goes up while Ernie's goes down. Their true rating difference should be 600 points. Let's see how long it takes to get there.
The first chart below shows how the ratings change when no ramp up is used. You can see that it takes over 1000 matches to achieve the 600-point rating difference.
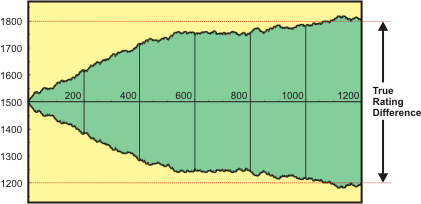
The second chart shows the ratings change when a ramp-up is used. Now the players reach their expected 600-point rating difference in less than 300 matches.
|
|
|
Understanding Your Rating
|
|
It can take a several hundred matches to reach your true rating. Even then, ratings have natural random variation. Your rating is not a completely precise measure of ability.
If you go on a lucky streak and win several matches in a row, your rating will zoom up. This doesn't mean you suddenly became a brilliant player. More likely, you were just blessed with good dice that day. And the same thing can happen in the opposite direction—you go into a prolonged losing streak and your rating takes a dive.
However, over the long term, your rating will give you a pretty good idea of how you stack up against other players.
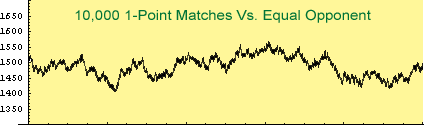
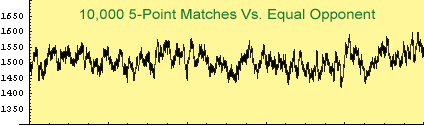
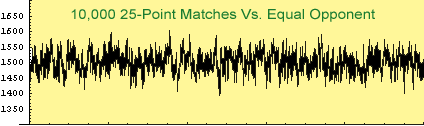
How much do the random fluctuations interfere with an accurate reading of your true rating? The following table gives an idea.
How Accurate is Your Rating?
| Accuracy | How Often |
| Within 10 points | 19 percent of the time |
| Within 20 points | 37 percent of the time |
| Within 30 points | 53 percent of the time |
| Within 40 points | 66 percent of the time |
| Within 50 points | 77 percent of the time |
| Within 60 points | 85 percent of the time |
| Within 70 points | 90 percent of the time |
| Within 80 points | 94 percent of the time |
| Within 90 points | 97 percent of the time |
| Within 100 points | 98 percent of the time |
|
|
|
Points-per-game (PPG) is a measure of the relative strength of two players. Play a series of games; take your net points won or lost; and divide by the number of games you played. That's your PPG versus that opponent.
Since both PPG and rating difference are measures of relative ability, you might expect there to be a relationship between the two. David Montgomery has studied this (see this post). He estimates that a win rate of 0.10 ppg corresponds to a rating difference of 40-50 points.
|
|
|
Ratings Manipulation
|
|
Most people just play backgammon and do their best to win. It's fun to see what kind of rating you end up with and try to improve your game over time. But a few people like to "play the rating system" and try to get their rating as high as possible by any means.
What can you do to artificially inflate your rating? Here are some possible tactics:
- Blatant cheating. The most direct way to give yourself a high rating is to cheat. One way of cheating is to set up two accounts on the same play site and dump games from one account to the other. Another is to leave a match when you are about to lose to avoid being charged with the loss. Cheating is against the rules (of course), and if it doesn't get you kicked off the server it will certainly make you unpopular.
- Play only one-point matches. The rating formula does not fully account for the skill involved in a one-point match. If you are a good player, you will receive more rating points over the long term by playing only one-pointers against weaker opponents.
- Play new players. Most players are overrated at 1500 when they first start to play. Eventually their rating goes down to its proper level, but in the meantime you can benefit by playing them.
- Play people who are currently overrated. Everyone's rating goes through swings of good luck and bad luck. If you can identify players who are currently overrated, you can benefit by playing against them. How can you find such players? One way is to track their rating over a period of time and look for a sudden increase. Another is just observe how they play. Sometimes you can tell that a player doesn't seem to play as well as his rating suggests.
|
|
|
A dropper is a player who intentionally leaves a match he is about to lose to avoid being charged with a loss. This is cheating of course.
|
|
|
A 99-in-1 match is a one-game match for 99 points (the maximum length you can play on FIBS). Two players agree ahead of time to send the doubling cube back and forth until the it reaches 128. This guarantees that the match will decided in its first game. Some people find these all-in-one matches exciting because of the large amount of ratings at stake. But 99-in-1 matches are sometimes a sign of cheating, so they are frowned upon or not allowed at all.
|
|
Formulas for Rating Changes
|
|
During Ramp Up
(E < 400) |
After Ramp Up
(E > 400) |
Points Added
To Your Rating
After a Win |
 |
 |
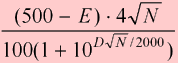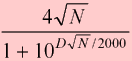Points Deducted
From Your Rating
After a Loss |
 |
 |
|
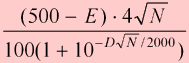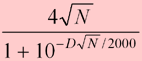D = rating difference: your rating minus opponent's rating
N = match length
E = experience: the total length of matches completed
|
|
Return to
: Backgammon Galore
: FAQ
|
