
By Tom Keith.
Last updated 25 November 1995.
Your feedback is appreciated!
Please send suggestions, comments, or questions to
tom@bkgm.com.
When backgammon tournaments are held to determine an overall winner, the usual style of competition is match play. Competitors are paired off, and each pair plays a series of games to decide which player progresses to the next round of the tournament. This series of games is called a match.
Matches are played to a predetermined specified number of points. The first player to accumulate the required number of points wins the match. Points are awarded: one for a single game, two for a gammon, and three for a backgammon. The doubling cube is used, so the number of points a player receives is multiplied by the value of the cube. Automatic doubles, beavers, and the Jacoby rule are not used in match play.
We should emphasize that there is no bonus for winning more than the required number of points in a match. The players' sole goal is to win the match, and the final score is immaterial. This can lead to some apparent inequities.
Consider a three-point match which one player leads 2 to 1. The player with 2 points would seem to have a significant advantage until you realize the strategy available to the player with 1 point. That player will simply double at his first opportunity in the next game. The player with 2 points is then forced to either (1) accept the double, in which case that game will decide the match, or (2) refuse the double, giving up a point, so that the following game decides the match.
This situation has lead to the adoption of a rule called the Crawford rule. The Crawford rule states that if one player reaches a score one point short of the match, neither player may offer a double in the immediately following game. This one game without doubling is called the Crawford game. After the Crawford game, if the match has not yet been decided, the doubling cube becomes available again.
It is convenient when discussing doubling strategy to refer to match scores in terms of the number of additional points each player needs, rather than the number of points they have won so far. For example, when one player leads a 7-point match 5 to 4, we would say that the score is 2-away, 3-away, meaning that the player with 5 points is 2 points away from victory and the player with 4 points is 3 away from victory. This is called a normalized score.
The advantage of normalized scoring, is that it is not necessary to know the length of a match to be able to determine either player's chances of winning. It allows us to talk about whole classes of scores for which the same doubling strategy applies.
Normalized scores are sometimes written with minus signs to distinguish them from scores expressed in terms of points won. For example, the score is -7,-7 at the start of a seven-point match or when each player has won 4 points in an 11-point match.
In the Crawford game itself, doubling strategy is very simple: neither player is allowed to double, so there are no decisions to be made! But after the Crawford game, the cube is in play again.
The trailing player should double in any post-Crawford game at his earliest opportunity. After all, he has nothing to lose; if he loses the game, he will lose the match anyway. By doubling early, the trailing player guarantees that each game is worth two points (maybe four if it is a gammon). This early double by the trailing player in a post-Crawford game is called a mandatory double.
What about the leading player? When he is offered a mandatory double, should he accept?
If the trailing player has an odd number of points to go (e.g., he is at 3-away or 5-away), then the leader should definitely accept the mandatory double. Refusing would reduce the number of games the trailing player needs to win the match.
If the trailing player has an even number of points to go (e.g., he is at 2-away or 4-away), then the leader has a choice. Suppose the match score is 1-away, 2-away. When the trailing player offers a mandatory double, the leader may either accept the double and let the current game decide the match, or he may refuse and let the next game decide the match. His best strategy, therefore, is to accept if he is ahead in the current game and refuse if he is behind. This option of being able to refuse a double when your opponent is an even number of points from victory is called a free drop.
In match play, the strategy you employ in doubling depends a lot on the score of the match. When you are behind in the match, you are more eager to double. You don't have as much to lose because the chances favor your losing the match anyway. By pushing the cube higher, you lessen the importance of past games, where you didn't do so well, and increase the importance of the present and future games where at least you have an even chance.
Similarly, when you are ahead in the match you must be more conservative with your doubling decisions. You are more reluctant to offer or accept the cube than when the match is even or when you are losing. When you are ahead, the odds are in your favor and you can increase those odds by playing many low-point games and avoiding high-point ones.
Suppose you know your probability of winning the present game. How can you use this information to help you decide whether or not to offer a double? Or when the cube has been offered to you, how do you choose whether to accept or refuse?
Perhaps you judge your chances of winning the present game to be 25%. (If the present game is played to conclusion, you expect to win 25 percent of the time and lose the other 75 percent of the time.) If your opponent doubles, should you accept? The answer depends, among other things, on the score of the match.
We will refer to the range of win probabilities at which either player should accept if offered a double as the market window.

Knowing the market window for the current match score can be very helpful in making doubling decisions. It tells you (1) whether to accept when your opponent offers a double, and (2) whether your opponent is likely to accept when you offer a double.
The following table shows the range of the market window at various match scores.
Opponent
2-away 3-away 4-away 5-away 6-away 7-away 8-away 9-away 10-awy 11-awy 12-awy
Player ----------------------------------------------------------------------------
2-away 30-70 34-75 33-83 30-81 29-84 32-84 30-88 31-86 29-88 32-87 30-89
3-away 25-66 28-72 29-76 27-78 28-79 30-82 29-83 30-84 29-84 31-85 29-86
4-away 17-67 24-71 26-74 26-75 26-76 28-77 28-79 28-79 28-80 29-81 29-82
5-away 19-70 22-73 25-74 25-75 26-76 27-78 27-79 28-79 28-80 29-81 28-81
6-away 16-71 21-72 24-74 24-74 25-75 26-76 27-77 27-77 27-78 28-79 28-79
7-away 16-68 18-70 23-72 22-73 24-74 25-75 26-76 26-77 26-77 27-78 27-78
8-away 12-70 17-71 21-72 21-73 23-73 24-74 25-75 25-76 26-76 26-77 27-77
9-away 14-69 16-70 21-72 21-72 23-73 23-74 24-75 25-75 25-76 26-77 26-77
10-away 12-71 16-71 20-72 20-72 22-73 23-74 24-74 24-75 25-75 25-76 25-76
11-away 13-68 15-69 19-71 19-71 21-72 22-73 23-74 23-74 24-75 25-75 25-76
12-away 11-70 14-71 18-71 19-72 21-72 22-73 23-73 23-74 24-75 24-75 25-75
For example, suppose you are leading the match at 2-away, 3-away. (You are two points away from winning the match; your opponent is three points away.) The relevant entry from the table above is "34-75". The "34" means you should refuse if you are offered a double when your probability of winning the game is less than 34%. The "75" means your opponent should refuse if he is offered a double when your probability of winning the game is greater than 75% (i.e., when his probability of winning is less than 25%).
Compare this with the situation when you are behind 3-away, 2-away. Now you can accept a double any time your winning chances are more than 25%, and your opponent must refuse any time your winning chances are more than 66%.
Factors other than the score of the match can change the position of the market window, so you should use the numbers above only as a rough guide. But this table contains a lot of useful information. Take some time to get a feel for the location of the doubling window at different match scores.
An important factor to consider when making doubling decisions is the potential for gammons. The calculations used to produce the Market Window Table assume that 20 percent of all games will end in a gammon. In your particular game, you may have a better idea how likely the chances of a gammon really are. Perhaps you and your opponent are in a close race, and there is almost no chance of a gammon. Or maybe one of you is playing a back game, and the chance of a gammon is much higher than normal.
As a general rule, the market window gets narrower as the chances of a gammon increase. As an example, suppose you are leading a match at 2-away, 4-away. The following chart shows how the market window shrinks for your opponent as the potential for gammon increases.
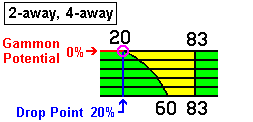
The chart says that with no chance of a gammon you may accept a double when your probability of winning the game is as little as 20%. But as the possibility of a gammon increases you must be much more cautious about accepting doubles. Look at the market window when your chance of gammon is 40%.
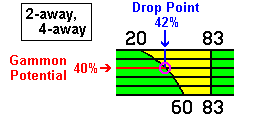
Now you should not accept a double unless your probability of winning the game is at least 42%. The reason you are more cautious here is that you don't want to give your opponent a chance to win a doubled gammon -- at this score, a doubled gammon is just what he needs to win the match.
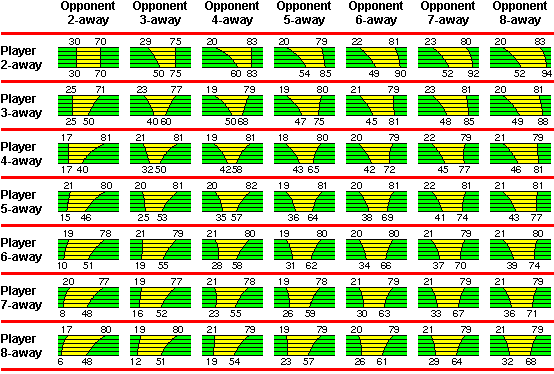
Here is a table of charts for all the match scores up to 8-away. Each chart shows how the position of the market window changes as the probability of gammon rises from zero (at the top of the chart) to 100% (at the bottom).
The decision of when to offer a double is always more difficult than the decision of whether to accept or refuse. The problem is volatility. Your situation in the game may change considerably from one chance to double to the next.
The best time to double is at the top of your market -- when it would be correct for your opponent to either accept or refuse. But such an opportunity almost never arises. You have to either double early (when your opponent should accept), or late (when your opponent should refuse).
Any time you are very close to the top of the market window, it is almost certainly correct to double. And, of course, if you are beyond the opponent's drop point, you should definitely double and take the sure point (unless there is a significant chance of a gammon). But what about before the opponent's drop point, while the opponent still has a clear take?
One way to view the doubling decision is that there is a cost associated with any double which is not made at exactly the top of the market window. When you double early, you give the opponent the cube at a time when he still has a good chance of using it against you. When you double late, you are not getting the maximum possible leverage out of your double.
The early/late cost ratio compares the cost of doubling early with the cost of doubling late. When the early/late cost ratio is low, you are more willing to double early to avoid the possibility of overshooting the opponent's drop point by a significant amount. When the ratio is high, you prefer to be very close to the opponent's drop point before offering a double.
The following table shows the cost ratios at various match scores.
Opponent
2-away 3-away 4-away 5-away 6-away 7-away 8-away 9-away 10-away
Player ------ ------ ------ ------ ------ ------ ------ ------ -------
2-away .0 .6 1.1 1.2 1.1 1.5 1.7 1.6 1.3
3-away .2 .7 1.0 .9 .9 1.0 1.2 1.1 1.0
4-away .3 .6 .9 .8 .8 .9 1.0 1.0 .9
5-away .3 .4 .6 .6 .6 .7 .8 .8 .8
6-away .2 .3 .5 .5 .5 .6 .7 .7 .7
7-away .3 .3 .4 .4 .5 .5 .6 .6 .7
8-away .3 .3 .4 .4 .4 .5 .5 .6 .6
9-away .3 .3 .3 .3 .4 .4 .5 .5 .6
10-away .2 .3 .3 .3 .4 .4 .5 .5 .5
As a general rule, it is better to double early (while you still have a take) than to double late. This is especially true when you are behind in the match, and particularly when the opponent is two points away from winning.
Take the case when you are trailing a match at 6-away, 2-away. The Market Window Table says the ideal time to offer a double is when you have a 71 percent chance of winning the game. But it turns out you can afford to double much earlier than this with very little cost. The early/late cost ratio at this score is so low (only 0.2), that you much prefer to double earlier than 71% than risk the possibility of having your double refused.
When you are well ahead in the match, you must be more careful about doubling early. You want to wait until the point where you have a good chance of overshooting the market by a signficant amount if you do not double now.
Look at the early/late cost ratio when the match score is 2-away, 2-away. The cost of doubling early is zero! This means that it is correct for either player to double (and for both players to accept) any time the probability of winning is within the market window -- between 30 and 70 percent.
At this score, you definitely want to be sure to double while your opponent is still willing to accept. In fact, at 2-away, 2-away, you can double on your first turn! If both players realize this and play accordingly, you can expect the 2-away, 2-away game to be the last game of the match.
The calculations used to determine the Market Window Table assume that the opponent will be able to make an efficient redouble if the game turns around and he starts to win. (By "efficient redouble," we mean that the opponent will be able to redouble at exactly the win probability that is best for him.) But a player may double only at his own turn, and a lot can happen between one doubling opportunity and the next. These volatility considerations mean that the opponent's redouble will usually not be 100 percent efficient. So the opponent's true recube vigorish is not as high as we have assumed. In fact, the ranges in the Market Window Table generally overestimate the size of the market window by about one or two percent.
The most extreme case of volatility is a last roll position. A last roll position is one where the next roll of the dice determines the outcome of the game. In a last roll position your opponent has no worthwhile chance to redouble, so his recube vigorish is zero. In this case, you may be better off not using the Market Window Table to make your doubling decision, and instead do the calculations yourself based on a match equity table.
A match equity table shows a player's expectation of winning or losing the match from any given score. Our table expresses match equity as a value between -1 and +1. A value of +1 means certain victory, -1 a sure loss, and 0 means that the player is equally likely to win or lose the match. (For information on how this table was calculated, see the accompanying article, "How to Compute a Match Equity Table.")
Opponent
1- 2- 3- 4- 5- 6- 7- 8- 9- 10- 11- 12-
away away away away away away away away away away away away
Player ---- ---- ---- ---- ---- ---- ---- ---- ---- ---- ---- ----
1-away .00 +.40 +.51 +.66 +.71 +.81 +.84 +.89 +.91 +.94 +.95 +.96
2-away -.40 .00 +.19 +.35 +.49 +.61 +.69 +.76 +.81 +.85 +.88 +.91
3-away -.51 -.19 .00 +.16 +.31 +.44 +.54 +.62 +.69 +.75 +.80 +.84
4-away -.66 -.35 -.16 .00 +.15 +.29 +.40 +.50 +.58 +.65 +.71 +.76
5-away -.71 -.49 -.31 -.15 .00 +.14 +.26 +.36 +.46 +.54 +.61 +.67
6-away -.81 -.61 -.44 -.29 -.14 .00 +.12 +.23 +.34 +.43 +.51 +.58
7-away -.84 -.69 -.54 -.40 -.26 -.12 .00 +.11 +.22 +.32 +.40 +.48
8-away -.89 -.76 -.62 -.50 -.36 -.23 -.11 .00 +.11 +.21 +.30 +.38
9-away -.91 -.81 -.69 -.58 -.46 -.34 -.22 -.11 .00 +.10 +.20 +.28
10-away -.94 -.85 -.75 -.65 -.54 -.43 -.32 -.21 -.10 .00 +.10 +.19
11-away -.95 -.88 -.80 -.71 -.61 -.51 -.40 -.30 -.20 -.10 .00 +.09
12-away -.96 -.91 -.84 -.76 -.67 -.58 -.48 -.38 -.28 -.19 -.09 .00
Let's see how to use the Match Equity Table to decide whether or not to offer a double in a last roll position. Suppose you are leading a match at 4-away, 6-away, and the current game will be decided by your next roll. You expect to win the game with 19 out of your 36 possible rolls, and expect to lose otherwise. The cube is at 1. Should you double?
To find out, first look up the match equities of the scores that result if you do not double, multiply each by its probability of occurrence, and add the products together. Compare this with the same computation done using the scores that result when you double and your opponent accepts.
If you do not double:
Result Match Score Match Equity Probability Value
----------------------------------------------------------------
You Win 3-away, 6-away +.44 x 19/36 = .2322
You Lose 4-away, 5-away +.15 x 17/36 = .0708
----------------------------------------------------------------
Expected Match Equity 36/36 .3030
If you double and opponent accepts:
Result Match Score Match Equity Probability Value
----------------------------------------------------------------
You Win 2-away, 6-away +.61 x 19/36 = .3219
You Lose 4-away, 4-away .00 x 17/36 = .0
----------------------------------------------------------------
Expected Match Equity 36/36 .3219
These calculations indicate that you are better off to double in this situation because doubling yields a higher expected match equity. The other possibility -- that your opponent could refuse your double -- is not likely because that would put the score at 3-away, 6-away. At that score, your match equity is +.44, which is much higher (and therefore worse for the opponent) than if he were to accept.
Everything we have said so far about doubling in match play applies to the first double of a game, but what about redoubles? In money play, a player's drop point is the same regardless of the level of the cube. But not in match play. Just as with gammon potential, the level of the cube affects when you should offer a double and whether you should accept. We therefore present a special market window table to be used for redoubles to the 4 level.
Opponent
2-away 3-away 4-away 5-away 6-away 7-away 8-away 9-away 10-awy 11-awy 12-awy
Player ------ ------ ------ ------ ------ ------ ------ ------ ------ ------ ------
2-away 0-100 30-100 50-100 47-100 46-100 51-100 58-100 55-100 53-100 53-100 55-100
3-away 0-70 25-75 40-83 38-85 38-90 42-92 48-94 46-94 45-95 46-96 48-97
4-away 0-50 17-60 32-68 33-75 33-81 36-85 41-88 41-89 40-90 41-91 43-93
5-away 0-53 15-62 25-67 27-73 28-77 32-82 36-84 36-86 37-87 38-88 39-90
6-away 0-54 10-62 19-67 23-72 25-75 28-79 32-82 33-83 34-85 35-86 37-87
7-away 0-49 8-58 15-64 18-68 21-72 25-75 28-79 30-80 31-82 32-83 34-85
8-away 0-42 6-52 12-59 16-64 18-68 21-72 25-75 27-77 28-79 30-81 31-82
9-away 0-45 6-54 11-59 14-64 17-67 20-70 23-73 25-75 26-77 28-79 29-80
10-away 0-47 5-55 10-60 13-63 15-66 18-69 21-72 23-74 25-75 26-77 28-79
11-away 0-47 4-54 9-59 12-62 14-65 17-68 19-70 21-72 23-74 25-75 26-77
12-away 0-45 3-52 7-57 10-61 13-63 15-66 18-69 20-71 21-72 23-74 25-75
Notice that the first column and first row of this table are very different than the regular Market Window Table. If your opponent is only two points away from winning the match and he redoubles, you cannot afford to refuse the double under any circumstances.
Gammon potential has a large effect on the market window when the cube is at this higher level, so always be aware of the possibility of a gammon and adjust your doubling decisions accordingly.
We have presented a lot of information here, but the basic principles of doubling in match play are actually quite simple. Remember that for most scores, especially when both players have a long way to go, doubling strategy in match play is quite similar to money play. Here are the main points to remember:
If you would like more information on making doubling decisions in match play, I recommend Kit Woolsey's book "How to Play Tournament Backgammon" (50 pages, $20). It is available from The Gammon Press, P.O. Box 294, Arlington, MA 02174.
In this monograph, Woolsey presents his widely-regarded match equity table and shows how to use it to make doubling decisions at various scores. He discusses the effects of cube leverage and gammon potential on doubling decisions and checker play. There are a number of examples. The book concludes with an exciting game between Woolsey and Bill Robertie that illustrates the techniques.