By Tom Keith
A match equity table is a useful to tool for making doubling decisions in match play. It shows a player's advantage or disadvantage at a given match score. You can use this information to compare the effect of doubling versus not doubling, or of accepting versus refusing when you are offered a double.
For information on how to use a match equity table, see:
Match equity refers to a player's expectation of winning a match. The measure of equity we use assigns a value of +1 to the condition when a player is certain to win the match, -1 when he is certain to lose the match, and 0 when he is equally likely to win or lose. At any given time, a player's and the opponent's equity sum to zero.
You will often see match equity stated elsewhere in terms of a player's probability of winning the match. The reason we use a "plus/minus" equity rather than the probability of winning the match is that, in discussions of match play doubling strategy, we will also refer to a player's probability of winning the present game. Dealing with two different probabilities (that of winning the game and that of winning the match) can be confusing, so we prefer not to use probability for match equity.
We make the following assumptions in our calculations:
It is necessary to compute match equities backwards, starting with the games at the end of the match, because the equity before any given game depends on the equities of the scores that can result. Therefore, we will start our calculations with the games played after the Crawford game.
In a post-Crawford game, the leading player is one point away from victory and the other player is one or more points from victory. The doubling cube is available to be used.
At 1-away, 1-away, the match is even, so match equity is zero for both players.
At 1-away, 2-away, the leader has a slight advantage because when the trailing player doubles the leader has the option of refusing if he is behind in the game (he has a free drop). We assume the leader's equity at this score is +.02.
At 1-away, 3-away, the trailer will double at his first opportunity. The leader will accept and never redouble. So there are four possible results. They are listed below from the leader's point of view, together with their probability of occurrence.
Leader's Outcome New Score Equity Probability Value ----------------------------------------------------------------- Win 2 x Gammon 0-away, 3-away +1 x 10% = +.1 Win 2 x Single 0-away, 3-away +1 x 40% = +.4 Lose 2 x Single 1-away, 1-away 0 x 40% = .0 Lose 2 x Gammon 1-away, 0-away -1 x 10% = -.1 ----------------------------------------------------------------- Leader's Equity 100% +.4
The leader's equity is the sum of the possible resulting equities with each result multiplied by its probability of occurrence. This yields a post-Crawford equity at 1-away, 3-away of +0.4.
At 1-away, 4-away, the leader also has a free drop, but he is less likely to use it here than at 1-away, 2-away: If the leader has only a mildly bad start to the game, he will prefer to save the free drop in case he needs it at 1-away, 2-away. The leader actually has a free drop whenever the trailer is an even number of points from victory. But he can use a free drop only once. So there is little additional contribution of free drop vigorish at scores where the trailer is four or more points from winning.
In general, we use the following steps to calculate post-Crawford match equity: (1) List the possible outcomes and the resulting equities. (2) Multiply each equity by its probability of occurrence. (3) Take the sum.
Here are all the equities of the post-Crawford scores up to 12-away.
Leader's
Post-Crawford Score Match Equity
------------------------------------
1-away, 1-away .00
1-away, 2-away +.02
1-away, 3-away +.40
1-away, 4-away +.42
1-away, 5-away +.66
1-away, 6-away +.67
1-away, 7-away +.80
1-away, 8-away +.81
1-away, 9-away +.89
1-away, 10-away +.89
1-away, 11-away +.94
1-away, 12-away +.94
Once the post-Crawford equities have been computed, we can compute the equities for all Crawford game scores. These values will become the first column and first row of the match equity table.
The process is similar to the way the post-Crawford equities are calculated. But, there are two important things to keep two things in mind: (1) There is no doubling in the Crawford game. (2) The input values to the Crawford game calculations come from the post-Crawford equities computed above, not from the Crawford game equities.
Here is an example for 1-away, 3-away (Crawford). For each possible (post-Crawford) outcome, we find the resulting score, look up the equity from the list above, and multiply it by its probability of occurrence. Then we take the sum of the results.
Leader's Outcome New Score Equity Probability Value ------------------------------------------------------------------ Win Gammon 0-away, 3-away +1 x 10% = +.10 Win Single 0-away, 3-away +1 x 40% = +.40 Lose Single 1-away, 2-away +0.02 x 40% = +.008 Lose Gammon 1-away, 1-away 0 x 10% = .00 ------------------------------------------------------------------ Leader's Equity 100% +.508
After rounding to two digits, we enter the value +.51 into the match equity table for the score 1-away, 3-away.
When all the Crawford game equites have been calculated and entered, the partially completed match equity table looks like this:
Opponent
1- 2- 3- 4- 5- 6- 7- 8- 9- 10- 11- 12-
away away away away away away away away away away away away
Player ---- ---- ---- ---- ---- ---- ---- ---- ---- ---- ---- ----
1-away .00 +.40 +.51 +.66 +.71 +.81 +.84 +.89 +.91 +.94 +.95 +.96
2-away -.40 .00 ? ? ? ? ? ? ? ? ? ?
3-away -.51 ? .00 ? ? ? ? ? ? ? ? ?
4-away -.66 ? ? .00 ? ? ? ? ? ? ? ?
5-away -.71 ? ? ? .00 ? ? ? ? ? ? ?
6-away -.81 ? ? ? ? .00 ? ? ? ? ? ?
7-away -.84 ? ? ? ? ? .00 ? ? ? ? ?
8-away -.89 ? ? ? ? ? ? .00 ? ? ? ?
9-away -.91 ? ? ? ? ? ? ? .00 ? ? ?
10-away -.94 ? ? ? ? ? ? ? ? .00 ? ?
11-away -.95 ? ? ? ? ? ? ? ? ? .00 ?
12-away -.96 ? ? ? ? ? ? ? ? ? ? .00
Regular game equities are harder to compute because the doubling cube is in play. Our general approach is to start with the cube at a high level, when the relationship between match equity and probability of winning the game is obvious. From there, we figure out the match equity when the cube is one level lower and repeat the process until we know the match equity when the cube is at the 1 level, before either player has doubled. The value we enter into the match equity table is the equity when the cube is in the middle and both players' probability of winning is 50%.
There is a useful property which applies because of our assumption of efficient doubles: For any given match score and state of the cube, a player's match equity is a linear function of his probability of winning the game. We will use this property over and over again in the process of deriving match equities.
The easiest way to see how equity calculations are performed is with an example. We will show how to calculate the match equity for one player ("Player") when that player is 2 points away winning the match and his opponent ("Opponent") is 3 points away. We already know the equities of all scores that can possibly result from this game.
What we want to find out is the match equity at the start of the game -- when the cube is centered and both players' probability of winning is 50%. This equity depends on when each player makes his first double. And the timing of the first doubles depends on when each player makes a redouble. Once the cube reaches the 4 level, there will be no further redoubles. So our investigation of match equity for this score starts with the cube at 4.
If the cube is at the 4 level when the score is 2-away, 3-away, there are more points on the cube than either player needs to win the match -- the winner of the game will also be the winner of the match. This makes the relationship between match equity and the probability of winning the game a very simple one.

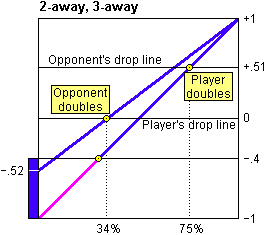
When Opponent owns the cube at 2 and things go badly for Player, then at some point Opponent will redouble to 4. Opponent will make this redouble when the match equity is the same whether the double is accepted or not.
If Player refuses the double, he loses two points and the match score becomes 2-away, 1-away with Player's equity becoming -0.4. If Player accepts the double, the cube ends up at the 4 level. Referring to the chart below, we can see that with a 4-level cube, Player's equity is -0.4 when his probability of winning is 30%. This is when Opponent will make his redouble.
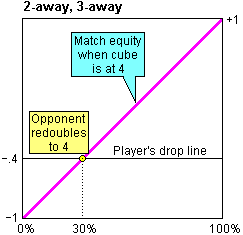
We also know that if things go well for Player when the cube is at 2, and Player wins the game, he will also win the match. So, at 100% win probability, Player's match equity is +1.
These two facts (that Player's equity is -0.4 at 30%, and +1 at 100%) allow us to plot Player's match equity when Opponent owns the cube at 2.
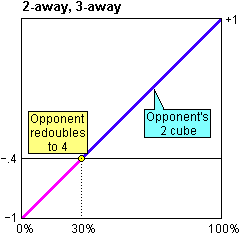
When Player owns the cube at 2 and things go badly for him, Opponent cannot use the cube against him. If Player loses a single game, he loses 2 points, which puts the match score at 2-away, 1-away (-0.4). If Player loses a gammon, then he loses the match (-1). We assume that 20% of all of Player's losses will be gammons. So, his average equity when he loses is
80% x (-0.4) + 20% x (-1) = -0.52
We have already noted that if things go well for Player when the cube is at 2, and Player wins the game, he will also win the match. Therefore Player's equity is -0.52 at 0%, and +1 at 100%. So now we can plot the match equity for when Player owns the cube at 2.
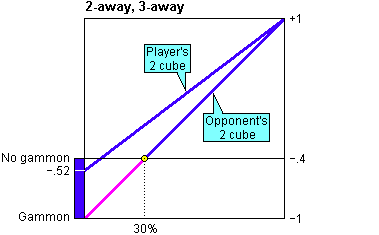
We are narrowing in on the target. From the chart above, we can tell for any given probability of winning the game the equity that results if either player doubles and the other accepts.
Now what if each player's double is refused? If Player doubles and Opponent refuses, the match score is 1-away, 3-away (+0.51). If Opponent doubles and Player refuses, the match score is 2-away, 2-away (0).
Each player will offer a double when the equity is the same whether the double is accepted or not. So Player will offer a double when his probability of winning is 75% and Opponent will offer a double when Player's probability of winning is 34%
We can join these two points with a line that represents match equity before the first double. With this line in place, we can look to see what the equity is at the start of the game, when the cube is in the middle and the probability of winning is 50%.
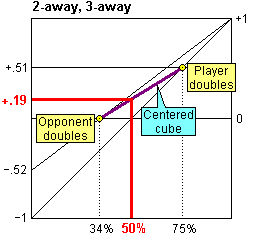
This value (+.19) is Player's match equity at the start of the game, and it is the value we enter into the match equity table at 2-away, 3-away. We can also enter the value -.19 at 3-away, 2-away.
The same technique can be used to compute all the remaining entries of the table. At higher away scores, the cube is not dead until it reaches 8 or 16, so there are more steps involved in the computations. But the method is the same.
Here is a final example showing the match equity calculations for when Player is 5-away and Opponent is 6-away.
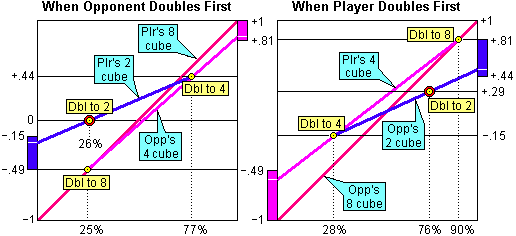
Once it has been determined where each player makes his initial double, we can plot the equity for a centered 1-cube and go on to find the match equity at the start of the game.
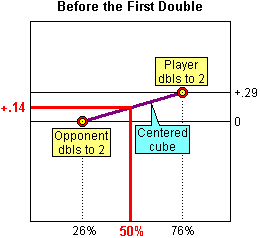
Opponent
1- 2- 3- 4- 5- 6- 7- 8- 9- 10- 11- 12-
away away away away away away away away away away away away
Player ---- ---- ---- ---- ---- ---- ---- ---- ---- ---- ---- ----
1-away .00 +.40 +.51 +.66 +.71 +.81 +.84 +.89 +.91 +.94 +.95 +.96
2-away -.40 .00 +.19 +.35 +.49 +.61 +.69 +.76 +.81 +.85 +.88 +.91
3-away -.51 -.19 .00 +.16 +.31 +.44 +.54 +.62 +.69 +.75 +.80 +.84
4-away -.66 -.35 -.16 .00 +.15 +.29 +.40 +.50 +.58 +.65 +.71 +.76
5-away -.71 -.49 -.31 -.15 .00 +.14 +.26 +.36 +.46 +.54 +.61 +.67
6-away -.81 -.61 -.44 -.29 -.14 .00 +.12 +.23 +.34 +.43 +.51 +.58
7-away -.84 -.69 -.54 -.40 -.26 -.12 .00 +.11 +.22 +.32 +.40 +.48
8-away -.89 -.76 -.62 -.50 -.36 -.23 -.11 .00 +.11 +.21 +.30 +.38
9-away -.91 -.81 -.69 -.58 -.46 -.34 -.22 -.11 .00 +.10 +.20 +.28
10-away -.94 -.85 -.75 -.65 -.54 -.43 -.32 -.21 -.10 .00 +.10 +.19
11-away -.95 -.88 -.80 -.71 -.61 -.51 -.40 -.30 -.20 -.10 .00 +.09
12-away -.96 -.91 -.84 -.76 -.67 -.58 -.48 -.38 -.28 -.19 -.09 .00
How accurate is this table? There must be some error because the assumptions we make (constant gammon rate of 20%, efficient doubling) are not really correct. But it is hard to say how much of a difference the assumptions make in the final values of the table.
It is encouraging to note that our table agrees quite closely with Kit Woolsey's widely-regarded match equity table [1]. (A copy of Woolsey's table appears in Stephen Turner's article "Calculating and Using Match Equities.") Woolsey uses a combination of mathematical analysis and emperical evidence extracted from a large database of matches to derive his table. His assumptions are based on experience of how people actually play and the results they achieve.
Most of the values in our table differ with Woolsey's by less than a percent. The largest difference is at 3-away, 8-away. Woolsey's table shows the leader has an 80 percent chance of winning the match. Our table would show an equity of +.624 if we did the calculations to 3 digits. This is equivalent to an 81.2% probability of winning the match -- a difference of 1.2%.
Norman Zadeh computed a match equity table in an article published in 1977 [2]. Our table also agrees closely with his. The largest difference in a pre-Crawford score is at 3-away, 6-away. Zadeh and Woolsey both put the probability of winning the match at this score at 71%, whereas our table shows an equity of +0.44, which is equivalent to 72%. Some of Zedah's Crawford-game equities differ from ours by more than a percent. This is because he assumes no free drop vigorish and he uses a higher gammon rate.
E-mail: tom@bkgm.com
Last Updated: 4 February 1997.