|
The literature provides detailed descriptions of the many methods available. Some commentators have suggested that it is possible to keep a running total of the pip count right from the beginning of the game. I personally found this technique unworkable. I soon lost count and the constant mental processing involved distracted me from concentrating on other important aspects of the game. Magriel highlights three distinct methods to calculate the pip count: The Direct, The Comparison, and The Mental Shift techniques (Magriel, at pages 126 to 131).
Other experts such as Jack Kissane have publicized other effective techniques such as the application of "reference positions". The Kissane methods are set out in detail at Backgammon Galore. The article there was originally published in the Chicago Point, Issue 52, November 1992.
Each of the above methods requires some basic mathematical ability—adding, subtraction, and multiplication—and a decent memory. Some require recognition and/or visualization of basic reference positions. Concepts from one method may be applicable to the others. To decide which method is most suited to your personal style of mental processing, check out the references provided and give each a try.
A short cut, and technique, which I found to be very effective, is explained in detail below. I first came across the concept on the news group archives section of the Backgammon Galore web site. It was originally posted on the newsgroup by Mark Denihan, 7 October 1996. The site also lists many other articles which may be of interest.
The Quadrant Crossover Technique
For the purposes of this tutorial I will call this method the "Quadrant Crossover" technique. In essence, it requires only four simple skills:
- A fluency in the basic multiplication tables for the numbers from 1 to 5 and more extensive familiarity with the multiplication tables for the number 6 (for example multiples of 6 up to the multiplier of 25);
- Basic addition and subtraction skills;
- The ability to visualize moving a checker six points;
- The ability to remember a single two or three-figure number while undertaking the previous tasks.
However, this method has an added advantage for a beginner. The full technique can be quickly learnt by breaking down the process into easily mastered stages of gradually increasing difficulty. Furthermore, mastery of each stage is very useful in itself by giving the beginner progressively more detailed information of their race standing. Bonus! Knowledge is power.
Stage One
Initially, ignore all the checkers of both players that have made it home. Observe the number and position of the remaining checkers you have on the board. Count the number of crossovers required to bring each checker into the home board. A crossover is the move of a checker of six spaces (or pips) from one quadrant of the board to the next quadrant.
(It is important to note here that to simplify this tutorial, in the Example Position below, each opponent has cleared his checkers from his adversary's home board. However, in other situations there will definitely be times that you will have to calculate the crossovers for checkers that have yet to escape their opponents' home boards.)
 |
|
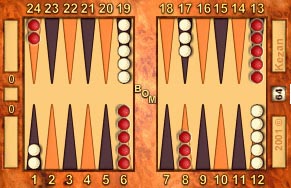
Example position, numbered from Red's perspective.
|
In the example position above, White has managed to escape Red's menacing prime. It is a racing position as there can be no further contact between the opponents' checkers in this game. Red has two checkers on the seven point, four on the eight point and one checker on the nine point. Therefore, Red needs 7 crossovers to bring all her checkers into the home board.
 |
|
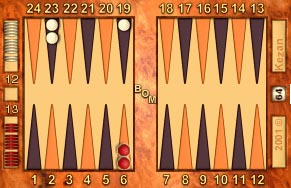
Same example position, numbered from White's perspective.
|
The view from White's side of the board (shown above) shows that 8 crossovers are needed to bring all her checkers home. Two crossovers for the checker on her 14 point, two more crossovers for each of the checkers on White's 13 point, plus one crossover for the checker on White's 12 and another for the checker on White's 7 point. Therefore we can deduce that Red is definitely leading the race by 1 crossover.
Since a crossover corresponds to a move of six pips we can deduce from this exercise that Red leads by one crossover or roughly 6 pips.
Stage Two
Now that we understand what a crossover is and how to calculate how many we need for all of our checkers to reach our homeboard, we need to visualize and remember where they land to be able to arrive at the exact pipcount.
However, before going to that step in the tutorial, sometimes just knowing how many crossovers you are ahead or behind allows you to clearly see your advantage or disadvantage especially in doubling situations.
To facilitate an improvement in the accuracy of this estimation, we must mentally move the checkers to see where they land. For example, if we pretend we are playing as Red in the Example Position below, we must consider that the white checker on the 13 point (White's 12) will land on White's 6 point and White will have three checkers to bear off from the 6 point.
On the other hand, if we now visualize where Red's checkers will land after Red does the crossovers and we compare, Red has only two checkers on the 6 point. This means that Red is in the lead by about 12 pips—six pips for the extra crossover and about six for the extra checker on the 6 point. Please note that these calculations are specific to this particular Example Position. In other scenarios, it will be plain to see that after the crossovers, the player with less checkers on his 6 and 5 points has the advantage:
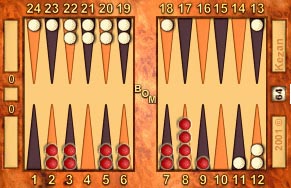 |
|
Example position, numbered from Red's perspective.
|
Stage Three
Beginners who have gained familiarity with the previous stages are now ready to calculate the exact pip count by including all the checkers on the board. Here is the example position again so that you don't have to scroll back up.
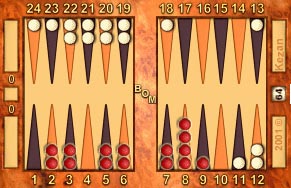 |
|
Example position, numbered from Red's perspective.
|
Start with your own checkers. Calculate the number of crossovers and include the checkers on the 6 point. Multiply by six to get the subtotal then add the remaining checkers from the 5 point onwards to obtain a total count. Don't forget to include the checkers from the crossovers when calculating the number of checkers on each home board point! Remember your total, and then repeat the exercise for your opponent's checkers. The difference between these two totals represents your exact standing in the race.
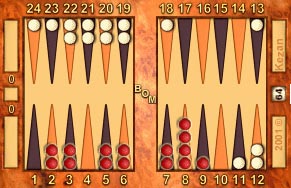
Here's the breakdown calculation for the Example Position for Red:
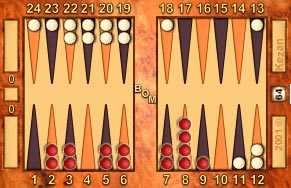 |
|
Example position, numbered from Red's perspective.
|
| Total crossovers plus the 6 point: |
9 × 6 = |
54 |
| Five point: |
2 × 5 = |
10 |
| Four point: |
0 × 4 = |
0 |
| Three point: |
3* × 3 = |
9 |
| Two point: |
6* × 2 = |
12 |
| One point: |
2* × 1 = |
2 |
|
|
|
|
|
87 |
* Note: The asterisks indicate points where outer board checkers have landed from the crossovers and have been added to the checkers already there.
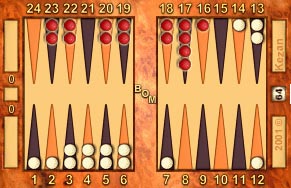
Here's the breakdown calculation for the Example Position for White:
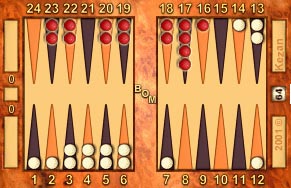 |
|
Same example position, numbered from White's perspective.
|
| Total crossovers plus the 6 point: |
11 × 6 = |
66 |
| Five point: |
2 × 5 = |
10 |
| Four point: |
2 × 4 = |
8 |
| Three point: |
2 × 3 = |
6 |
| Two point: |
2* × 2 = |
4 |
| One point: |
4* × 1 = |
4 |
|
|
|
|
|
98 |
* Note: The asterisks indicate points where outer board checkers have landed from the crossovers and have been added to the checkers already there.
From this full pip count we have verified that Red leads White by 11 pips, (98 − 87 = 11).
As previously mentioned, a player who can accurately calculate the pip count is in a position of power. In the example position, it is Red's turn to roll the dice. What is the correct doubling strategy for both players? Using Magriel's criteria (see above), this is a long race situation (approximately 100 pips). Therefore, this is a clear double for Red and an acceptable take for White. (A JellyFish analysis confirms this.)
| 




![]()