|
|
Racing Tactics |
The Magic Triangle
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| From Backgammon Times, Volume 4, Number 1, Spring 1984. |
| Black to play 2-2. |
In bearing off, many players do not know how to arrange their last two men correctly. On the surface, their proper placement seems to be without much rhyme or reason.
In response to this problem, some players have developed rules giving the preferred position when only two mean remain on the board. Unfortunately for the backgammon student, each rule has been unduly complicated or contained an exception that had to be memorized.
This situation led me to discover a simple approach with no exceptions: the "magic triangle." It works like this: Write the numbers 0 through 5 in an inverted V pattern as shown.
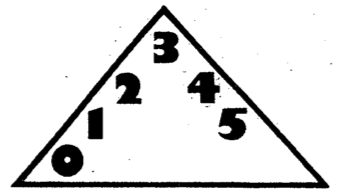
These numbers represent the spacing of the two remaining men. Spacing is defined as the difference in numerical value of the points on which the two men are located. For example, men on the 5 and 1-points have a spacing of 4; two men next to each other have a spacing of 1.
Read the numbers from left to right, top to bottom, just like a normal page. This gives the preference order of the spacings. Thus, 3 is always equal to or better than 2; 2 is always equal to or better than 4, etc.; and 0 (two men on the same point) is the worst.
The preference order applies only when the two remaining men are both in the home board. Also, it applies only in comparing positions with equal pip counts. For example, it means that you should prefer men on the 6 and 3-points over men on the 5 and 4-points (pip counts 9 each), but it does not mean that you should prefer men on the 6 and 3-points over men on the 3 and 2-points (pip counts 9 and 5 respectively).
In the diagram, Black has three ways to play the rest of his roll after he bears off a man from the 4-point. With each choice, the two remaining men wind up on a different pair of points. The three possible pairs are: (a) 6 and 1, (b) 5 and 2, and (c) 4 and 3. The spacings for each choice are: (a) 5, (b) 3, and (c) 1. The triangle indicates that 3, choice (b), is the best and Black should therefore play his 2-2 roll as 4/off, 6/2.
You can verify this preference order by examining the effect of each of the 36 possible rolls next turn. (Remember, a nondouble like 5-3 counts as two separate rolls: 5-3 and 3-5). With choice (b) 19 of the 36 rolls win for Black next turn. On the other hand, choice (a) produces only 17 winning rolls, and (c) only 15.
![]()
|
| More articles by Jeff Ward |
|
| More articles on racing tactics |
|
Return to: Backgammon Galore |
|