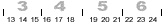|
As an intermediate player, I've had difficulties doing pip counts at the board. So much math, so many distractions. Too much mental fatigue for a player concentrating on basic checker moves. Yet, every text I read says the first thing you have to ask when evaluating a position is "What is the status of the race?—White's pip count is ...."
We read books in advance of our games so we don't have to figure out basic strategy at the board. We study reference doubling positions, 3-roll positions and opening moves in advance so we already know the most efficient move and can concentrate on finding subtle exceptions to the rule. What about taking the same approach to pip counting? Proper preparation allows you to reduce the mental effort needed to perform a pip count and lets you concentrate on the important issue—what to do with it.
There are several approaches to determining the status of the race. The quickest, but clearly the least accurate is to simply count the checkers on your 12th to 24th point and compare it to your opponents checkers on his/her 12th to 24th point. Quick but very inaccurate, you would do almost as well just eyeballing the board.
Another quick and slightly more accurate method is the crossover method. Since you want to get all your checkers home to bear off, you simply add up the checkers in the quadrant of the board between the 7th and 12th point and multiply them by 1 (they need one crossover to get to the home board), the checkers between the 13th and 18th point are multiplied by 2 (they need to cross over two quads to come home) and from the 19th to the 24th, they each need 3 crossovers so they count as three each. Simple, fast, useful and very easy to master. At the very least, do this and you can start to make some basic decisions with intelligence and logic.
The basic way to calculate a pip count in all the books is that you number the points on a board from 1 to 24, then count the number of checkers on each point and multiply that number by the number of the point. Then you add all those sums up and get a pip count. Again, on the opening position, there are 5 on the 6 point (30) plus 3 on the 8 point (24) plus 5 on the 13 point (65) plus 2 on the 24 point (48). Thus 30 + 24 + 65 + 48 = 167. This is very tedious, move a couple of times and theoretically you might have to add 15 numbers together in your head. Then you get to do the same for your opponent's board. Then remember back to what you got for yourself and compare the two. Not very practical.
One of the best articles I've read on pip counting is "The Half Crossover Method" by Douglas Zare. The basic premise is simple. Divide the crossovers in half (3 points each instead of the 6 points of the full crossover) and aim not for the entire home board, but for the 4, 5 and 6 points—more on that later.
|
|
|
Illustration 1.
A backgammon board with half crossovers marked.
|
Thus your checkers on the 8 point each have 1 half crossover to go, your midpoint checkers have 3 each and your back men 6 each. Not only can you get a much more accurate assessment of the race, by using a formula you can get a rough pip count. The Zare formula is (# of half crossovers × 3) + 75. Since in the starting position of the game there are 30 half crossovers, this gives a rough pip count of (30 × 3) + 75 = 165. Not bad and very little effort.
To diverge slightly, here is an analogy to what Zare did. To add all the numbers from 1 to 100 together without paper and pencil is a task that few can do. This is because most people would say: 1 + 2 = 3, 3 + 3 = 6, 6 + 4 = 10, .... A far better way is to look at it with fresh eyes and see a pattern. What about 1 + 100 = 101, 2 + 99 = 101, 3 + 98 = 101? Now the answer is simple: 101 × 50 = 5050. Done.
Zare's solution to the problem of the pip count is just as elegant. On an empty board, stack all 15 checkers on the 5 point, which is the midpoint of the home half crossover. What is the pip count? Let's see 15 × 5 = 75.
|
|
|
Illustration 2.
All 15 checkers on the five point: 75 pips.
|
That was easy. Now let's put 5 checkers each on the 4, 5 and 6 points. Now we have 20 + 25 + 30 = 75.
|
|
|
Illustration 3.
Also 75 pips.
|
There is that 75 again. How about any symmetrical formation on the 4, 5 and 6 points? Let's go with 7 each on the 4 and 6 points and 1 on the 5. That is 28 + 5 + 42 = 75.
|
|
|
Illustration 4.
Also 75 pips.
|
Now look at the midpoint of the first half crossover, the 8 point, and move the single checker from the 5 point in the last example there. Now we have 28 + 42 + 8 = 78. The Zare formula is now (1 half crossover × 3) + 75 = 78.
|
|
|
Illustration 5.
78 pips, 1 half crossover.
|
Move the checker on the 8 point to the 14 point (the midpoint of the 3rd half crossover). Now we have (3 half crossovers × 3) + 75 = 84.
|
|
|
Illustration 6.
84 pips, 3 half crossovers.
|
Now take one checker each from the 6 and 4 points and move them to join the checker on the 14. We now have 3 checkers with 3 half crossovers each so Zare tells us the rough pip count is (9 × 3) + 75 = 102.
|
|
|
Illustration 7.
102 pips, 9 half crossovers.
|
Confirming this we do it the old fashioned way and have 6 each on the 4 and 6 points (24 + 36) and 3 on the 14 (42) which total 102.
Returning to the original starting position of the board, we recall that several paragraphs ago we determined there were 30 half crossovers.
|
|
|
Illustration 8.
Red's checkers are 30 half crossovers from home.
|
Using the Zare formula we have (30 × 3) + 75 = 165. Close, but how do we correct to get the actual count of 167? Recall that the half crossover is based on a checker on the midpoint of the three point group. We used 8 for the 1st and 14 for the 3rd above. The midpoint of the 6th crossover is the 23 point.
|
|
|
Illustration 9.
The starting position with the midpoint of each half crossover marked.
|
At the start of the game the two back men are one point further back, so we have to add a total of 2 pips to our rough count to get 165 + 2 = 167, the final answer. If we rolled 1-1 from the start and decide to move both our back men from the 24 to the 22 point we would still have 30 half crossovers and a rough count of 165, but now we have our back men one point closer than the midpoint of the crossover and have to adjust our total to 165 − 2 = 163. Note that in both cases the extra 5 pips on the 6 point are equaled out by the 5 we have to take off for the checkers on the 13 point.
One last thing to look at, what about checkers in the home board or on the bar? Recall from the start of our discussion on the derivation of the Zare formula, our original example had all our checkers on the 4, 5 and 6 points. As they were home they had zero crossovers to go. If they were symmetrically placed about the midpoint of the home crossover (the 5 point) the pip count was (0 × 3) + 75 = 75.
Since checkers on the 1, 2, and 3 points are all one half crossover past our home crossover, they each count as −1 in our total half crossover count. Checkers on the bar have 7 half crossovers to get home (they are on the 25 point). Corrections for the final count are the same, remembering the midpoint of the bar "crossover" is the 26 point.
To summarize some key features of the Zare formula, we need to keep certain things in mind. First of all, you have to have 15 checkers on the board, including your men on the bar. Once you start taking men off, you can still use the formula, but you must subtract 5 pips from the total for each man taken off—going back to our original situation where all our men were on the 5 point, if we only had 14 men on the board it would be 14 × 5 = 70. Second, the Zare formula only gives a rough pip count, calculated from the midpoint of each half crossover. To get the exact pip count, we need to correct for checkers 1 pip past or 1 pip before each midpoint.
Why make the 4/5/6 points our home half crossover? We could use the 1/2/3 points and make the formula (# half crossovers × 3) + 30, or use the 7/8/9 points and use +120 in the formula. An interesting exercise would be to see how these constants of 30 and 120 are derived. Review the discussion of the standard 75 constant at the start of the article. To determine why the 4/5/6 points are the home crossover and not the 1/2/3 place 5 checkers each on the 4/5/6 points on one side of the board (75 pips) and on the opposite side place 4 each on the 1, 2 and 3 points and 3 on the 17 point (also 75 pips). Then roll the dice and bring the position home, using the same roll for both sides and repeat as many times as it takes to convince you of the wisdom of the 4/5/6 position.
|
|
|
Illustration 10.
The home half crossover shootout.
|
Now practice from the doubling problems in 501 Essential Backgammon Positions, by Robertie. Then continue to read and learn to use some "tricks" with the formula. Before learning the shortcuts, become very familiar with the base formula. Incorporate the half crossover count in your games, then get so you can calculate at least a rough pip count across the board.
In the final part of the article, we will examine shortcuts and tricks to make this formula very usable over the board.
Continue to Part 2
| 

![]()