The score is tied at 7 in a match to 11. Black is holding a 2-cube and is on roll. Should Black redouble? If Black redoubles, should White take?

Score: 4-away/4-away Should Black redouble to 4? Should White take?

I think this is a great position to illustrate just how interesting, complex, and complicated backgammon can be. We often have to make decisions about doubling and taking where all 30 checkers are on the board and there are many, many factors to consider, but here, there are only 4 checkers on the board and very few possible rolls left, and it's still not a simple decision! I will take you through the decision-making process the same way I would do it myself over the board, and then give you the answer. First, see what you would do as both Black and White yourself, and then read on.

The first question, and most obvious question is this: How often will Black win the game? Once you determine that, you obviously also know how often White will win the game (if Black wins 80% then White wins 20% for example).

Then once you determine winning odds, which is not all that simple to do by the way, you must then figure out if Black is better off holding the cube or giving it and risking the entire match on the next couple of rolls. And then if you decide it is worth the risk of giving the cube, you have to decide if White should just give up 2 points by dropping the cube or if he's better off playing on for the entire match right now.

So to answer the first question, we know Black wins immediate with the following rolls:

6-2, 2-6, 6-3, 3-6, 6-4, 4-6, 6-5, 5-6, 6-6, 5-5, 4-4, 3-3, 2-2. So 13 out of 36 rolls he wins on the first shake—that's 36% of the time. On the rest of the rolls, or the other 64% or other 23 rolls, he will lose if White bears off both his checkers on the next roll.

White will bear off both of his checkers with the following rolls: 6-2, 2-6, 6-3, 3-6, 6-4, 4-6, 6-5, 5-6, 5-2, 2-5, 5-3, 3-5, 5-4, 4-5, 6-6, 5-5, 4-4, 3-3, 2-2. That's 19 out of 36 rolls, or 52% that White wins, and 48% of the time he does not get off the board.

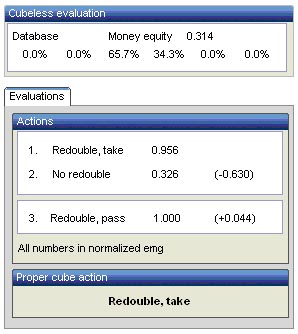
So Black wins 36% of the time immediately, and he doesn't lose 48% of the remaining 64%. So that's another 30%, and if you add that to his initial 36% wins, that means he wins around 66%. Now, that number does change very slightly because there is a possibility that either side could roll combinations of 1-1, 2-1 and 3-1 twice in a row and not get off in two rolls. So the actual winning percentage for Black is 65.7 percent. By the way, over the board I would not take the time to come up with this exact number, but I would take into account that there are some times both players don't get off in two rolls, and I know this will happen to Black more often than White because Black has one more pip to play than White.

Now, here's the next question. Even if you take the time and are able to accurately come up with 66%, or even quickly estimate that it is around that number (which is what most good players do over the board); should you double if you are Black?

The answer to me is not immediately clear, because it depends on what my winning odds (match equity) are if I win or lose without doubling.

In order to properly make this decision, you have to have an understanding of the match equities, or odds of winning and losing at various scores. As it happens, I do have such an understanding because I have studied this for many years and the match equity tables have been published in many books and articles and can be found in the computer software programs (Snowie, Jellyfish and GnuBG).

I know that at the current score, with each player 4-away from winning the match, we are both 50/50 to win the match at the beginning of the game. If I don't double and win 2 points, which the odds say would happen 66 percent of the time, I would then be 2-away and my opponent would be 4-away. At that score I happen to be a 66% favorite to win the match. And of course, if I lose, my opponent would be a 66% favorite. That tells me that if I am Black I should double, because either way I am 66%, and I always want to apply Woolsey's Law whenever I can.

Woolsey's Law simply states that if I am not sure, or on the edge, I should double. I might be making a mistake to double, and I might be making a mistake if I don't, but if I don't there is no way for my opponent to make a mistake!

So that answers the first question: Black should double. In fact, Snowie says it would be a blunder not to double—you'd rather play for the match when you are a 66% favorite, and you should put your opponent under the pressure of having to decide and possibly decide wrong.

Now, if you were White should you take? Again, your first question to answer is how often do I win, and if you do the math correctly, you will determine that you win about 1 out of 3 times, or 33 percent. If I take I lose the match 33% of the time, and if I drop, I still have only 33% chance to win, so I could really flip a coin here.

If White's checker on my 5 point was on my 6 point, it would be a huge error to take the cube. If White's checker was on the 4 point, it would be a huge error to drop the cube. If Black's checker on the 6 point was on the 5 point is would be a huge error for White to take the cube. One change of one pip for any one of the checkers would change the odds dramatically for both players.

This is why I love backgammon. It is far more interesting and complex than people realize. And this is why, in my opinion, all of the top players in the game are extremely intelligent people. It's not accident or coincidence. It takes brains to remember all the odds and match equities and to be able to figure all of this out in your head over the board and come up with the right answer and decision. Backgammon is not a fool's game!

By the way, in this position, Snowie says it is a clear double and a clear take and that is because the true odds, given the possible combinations of 1-1, 2-1, and 3-1 that could apply are 65.7 and 34.3 as you can see in the table below.