Half-Crossover Count
Douglas Zare created a method for counting pips which divides the board into octants, or "triples," as Zare calls them. The half-crossover pip count is described in this article.
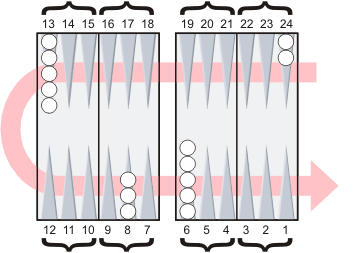
The half-crossover count is a two-stage process. First you do a rough count, focusing on the number of octants, or half-crossovers, the checkers must move to arrive in their home board. Then you fine tune the count, adjusting for the fact that some checkers are higher within their octant than others.
Kangaroo Count
The kangaroo count was devised by Nack Ballard. It is a variation of the half-crossover count and was first described in Issue #277 of the Flint Area BackgammoNews (Dec. 2005).
The easiest way to see how the kangaroo count works is by following an example. We will count White's checkers in the starting position of a new game.
Step 1.
|
Count up the checkers on the far side of the board and multiply by 2.
White has 7 checkers on the far side.
7 × 2 = 14.
|
|
|
Step 2.
|
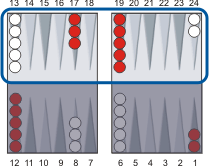
Add 1 for each checker on the major diagonal (see diagram) and double the resulting total.
White has 5 checkers on the major diagonal.
14 + 5 = 19, then 19 × 2 = 38.
|
|
|
Step 3.
|
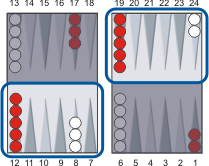
Add 1 for each checker on the minor diagonals (see diagram).
White has 7 checkers on the minor diagonals. 38 + 7 = 45.
|
|
|
Step 4.
|
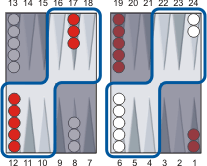
Multiply by 3 and add 30 to get the approximate pip count.
45 × 3 = 135, then 135 + 30 = 165.
This is White's approximate pip count.
|
|
The Kangaroo Poem
First you double the far side men.
Add big diagonal, double again.
Add small diags, times 3, plus 30,
And shifting to the middles is perty.
|
|
|
Fine Tuning
The last line of the poem refers to shifting to the middles and it is what you do to convert from an approximate pip count (as calculated above) to an exact count.
Checkers on the middle point of each octant are already accurately counted.
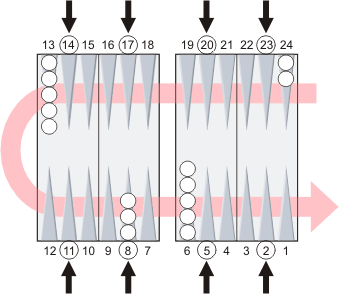 |
Middle points.
The three checkers on the 8 point are in the middle of their octant so they do not need any adjustment. |
Each checker on a heavy point adds one to the count.
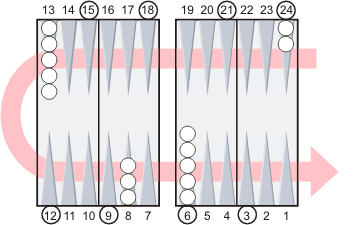 |
Heavy points.
The two checkers on the 24 point and the five checkers on the 6 point are on heavy points, so they add 2 + 5 = 7 pips to the count. |
Each checker on a light point deducts one from the count.
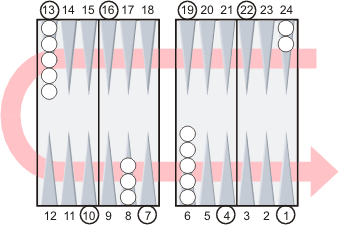 |
Light points.
The five checkers on the 13 point are on a light point, so they deduct 5 pips from the count. |
The approximate count computed above was 165. There are 7 checkers on heavy points and 5 checkers on light points. The exact pip count is therefore 165 + 7 − 5 = 167.
Compensating Shifts
You can often save yourself arithmetic by noticing piles of checkers that cancel each other out. The key to cancelling is to remember two rules:
- Cancellations on opposite sides of the board shift in the same direction.
- Cancellations on the same side of the board shift in opposite directions.
Here's the diagram again.
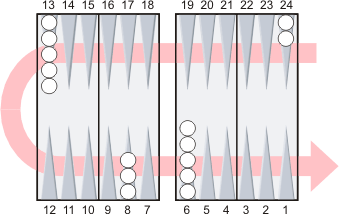
The five checkers on the 13-point need to move right to get to the middle of their octant.
The five checkers on the 6-point also need to move right to get to the middle of their octant.
Shifts on opposite sides of the board in the same direction cancel out, so we can ignore all ten of those checkers. That leaves only the two checkers on the heavy 24-point.
165 + 2 = 167.
Checkers on the Bar or Borne Off
Checkers on the bar or already borne off must be accounted for separately. Subract 2 for each borne off checker. Add 23 for each checker on the bar.
| 


![]()
