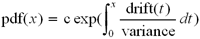
|
Ratings: A Mathematical Study
| |
by Douglas Zare
and Adam Stocks
|
This article originally appeared in GammonVillage in 2001.
Thank you to Douglas Zare for his kind permission to reproduce it here.
|
"If I am given a formula, and I am ignorant of its
meaning, it cannot teach me anything, but if I already know it what does the
formula teach me?"
—St. Augustine De Magistro ch X, 23.
|
|
Introduction
|
|
Although ratings systems are not directly part of backgammon, they are
common and interesting though frequently frustrating. In this article we
report some facts about the rating systems on three backgammon servers that
may increase the amount of information and enjoyment you get from
backgammon ratings. The questions we will address are as follows:
- If one is misrated, how long does that last?
- What is the half-life of a ratings difference? That is, how quickly
do ratings differences decay?
- How long does it take to bounce back to normal?
- How large are the normal swings of one's rating?
- How high should one's maximum rating ever be?
- Can one estimate someone's true rating from their experience level and
maximum rating?
- Finally, why do the answers given here differ from other answers in the
rec.games.backgammon
archive?
First, how do ratings work? There are many methods, but all of the ones we
will discuss have the property that there is a formula estimating the
probability of winning a match based on (1) the difference between the
ratings of the players and (2) the length of the match. One gains rating
points if one wins and loses rating points if one loses so that if the
formula's estimates are accurate, then on average, one's rating stays the
same. The number of rating points at stake also varies.
For example, suppose that on FIBS one plays a 25-point match
with a player
so much weaker that one has an 80% chance of winning. If this is accurately
reflected in the ratings, then when one wins, one will gain 4 rating points.
If one loses, one loses 16 points. Another way of thinking about this is
that one gives up 6 points before the match, and then plays for a stake of
10 points.
If your rating is very far from what it should be, then it will tend to move
closer to your playing strength. On the other hand, from the luck of the
dice your rating will fluctuate. In this article we will separate those
effects, determine the stable distribution of ratings, and show
that the maximum rating is often a better indicator of playing
strength than one's current rating.
|
|

|
1. The Half-Life
|
|
Suppose your rating suddenly drops by 100 points due to letting your
goldfish use your account or just a streak of bad luck. How long will this
change last? In some sense, the residue of the change will always be there,
but the effect will diminish with time, much like a radioactive substance
will decay.
Another way of thinking about the half-life is as follows: Your current
rating is a function of whether you won or lost in past games. More recent
games are more important than games played many experience points ago. The
half-life is how far back the matches worth only half as much as the most
recent matches are from the present.
What is the restoring force that pushes your rating toward its natural
level? Suppose that in the example above, you will only win 75% of the
25-point matches, so the fair payoffs are +5 and −15 rather
than +4 and −16.
Rather than paying 6 points to play for a stake of 10 points, the fair
amount is to pay 5 points, so you lose 1 point, and then play a fair game.
It doesn't matter much whether you win or lose that game.
Example:
Suppose players A and B play 5-point matches on FIBS against
players rated
1500, 1700, and 1600 in that order, and both of them win all 3 matches.
Player A starts with a rating of 1500. Player B starts with a rating of
1600.
|
Player A |
Player B |
| After match 1 |
1504.472 |
1603.900 |
| After match 2 |
1510.047 |
1608.922 |
| After match 3 |
1515.034 |
1613.343 |
So, after 3 matches, the rating of player A is less than that of player B by
98.309 rating points.
Suppose instead they lose all 3 matches.
|
Player A |
Player B |
| After match 1 |
1495.528 |
1594.955 |
| After match 2 |
1492.206 |
1591.084 |
| After match 3 |
1488.351 |
1586.663 |
After 3 matches, the rating of player A is less than that of player B by
98.313 points, almost exactly the same amount as if both had won all 3
matches! After another 100 5-point matches with the same
opponents (with
ratings near 1500) and the same results, player A and player B will probably
have ratings that differ by between 55 and 60 rating points.
The following graph illustrates the convergence of ratings in a simulation.
It shows the ratings on FIBS versus experience of accounts that start with a
range of rating, but have exactly the same pattern of opponents and wins and
losses. All opponents were assumed to be correctly rated at 1500. To
generate the sequence of wins and losses, it was assumed that
the actual playing strength was 1500.
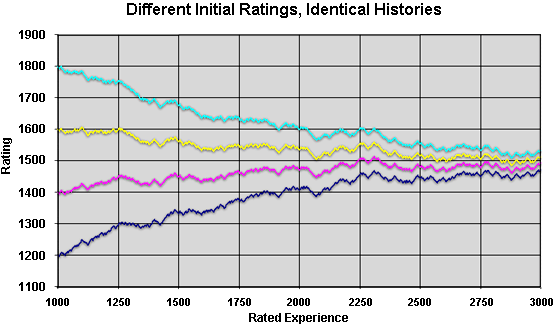
The restoring force is approximately proportionate to the length of the
match and to the difference between the ratings between player A and player
B, or between player A and the playing strength of A. These mean that it
makes sense to talk about a half-life of a ratings difference in units of
experience points, the sum of the lengths of matches that one plays. The
half-life varies slightly on the rating of one's opponent, the difference
between the two players' ratings, and the length of the matches. The
following table shows some empirically derived (from simulations) half-lives
for various values of each parameter:
server difference matchlength halflife
FIBS 300 5 605-655
FIBS 100 5 605-610
FIBS 10 5 605
FIBS 1 5 605
FIBS 100 1 602-604
FIBS 100 25 600-650
FIBS 100 5* 705-880
GGrid 100 1 641
GGrid 100 5 585-590
GGrid 100 25 575-625
GGrid 100 5* 650-760
GS2000 100 1 482-484
GS2000 100 5 485-495
GS2000 100 25 500-525
GS2000 100 5* 555-680
|
The lines with matchlength 5* give the half-lives when the opponent is 400
points weaker or stronger, rather than approximately equal to the player.
The opponent's rating and strength were chosen to be between the upper and lower
ratings that fit this description.
For example, this means that if two players on FIBS have ratings which
differ by 100 points play only 5-point matches with players of
about the
same rating, then after 121-122 matches (605-610
experience points) the
difference between the ratings will be just under 50 points if they have
the same pattern of wins and losses. Of course, if your true rating is 1500
and your actual rating is 1400, it is quite possible that after 600 exp,
your rating will still be 1400. However, for that to happen, you would have
to be unlucky to the extent that if your rating started at 1500 it would now
be about 1450. The 100 point gap from 1400 to 1500 has diminished to a 50
point gap between 1400 and 1450, and you have another 50 points of bad luck
to work off.
The values in the table don't differ from each other much. On FIBS, the
half-life varies from 600 to 650 for normal play. On GamesGrid, the
half-life varies from 575 to 641. On GameSite 2000, the
half-life varies from 482 to 525.
This can be varied slightly to give an approximate expected rating of a
player who goes through the "ramp" or initial adjustment period in which
the games are worth more. The ramped period of 400 experience
points is approximately equivalent to 1200 unramped experience points, or
about 2 half-lives on FIBS. So if a player's strength is 1600, then after
the ramped 400 experience points one expects that the rating has risen from
1500 to about 1575. On GamesGrid, the ramp lasts 500 experience points and
is about equivalent to 1500 experience points, or 2.5 half-lives, so a
player of strength 1800 can expect to be rated about 1747 after the
ramp.
The following graph shows the expected rating on GameGrid versus
experience, taking into account the ramp, and assuming that one plays
5-point matches against those whose (correct) ratings equal the
new player's nominal rating.
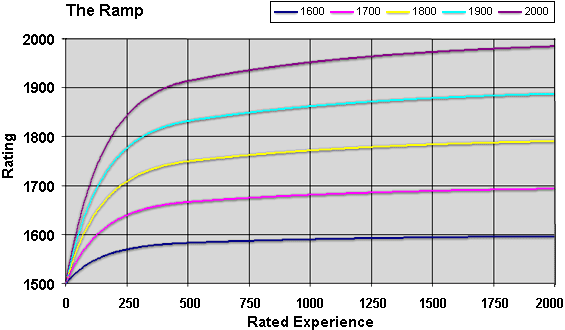
Incidentally, the restoring force is greatest when one plays people rated
half-way between one's rating and playing strength. Someone of playing
strength 1700 who is rated 1500 should play those correctly rated 1600 to
increase their rating as rapidly as possible.
|
|

|
2. How long does it take to bounce back from a fall?
|
|
A player, call her Double7 (not her real id), recently started playing on
GamesGrid with a rating of 1800 (and no ramp). Double7's play on
another server indicates that she actually should have been granted a rating
of at least 1900, and her rating quickly passed 1900. If we assume that
Double7's playing strength is 1900, how long should she wait before
her rating is first at least 1900?
Her expected rating will never be 1900, though it will be about 1850 after
600 exp, about 1875 after 1200 exp, etc. because of the half-life
phenomenon. She might encounter good luck and get a rating of 1900 after
only a few matches, or have enough bad luck that she does not reach 1850
even after 5000 exp. Although there are advanced mathematical tools that can
allow one to describe the distribution of the times before one reaches 1900,
the simplest method is just to simulate the process.
The following is a table of the 1st percentile, 10th percentile, 50th
percentile, 90th percentile, and 99th percentile times to bounce back from
various ratings differences assuming that one plays only 5-point matches against players with one's target rating using the GamesGrid formula. The sample sizes were 999, so the numbers may be off by a few percent.
delta 1st 10th 50th 90th 99th
20 25 45 215 1360 3185
50 95 200 675 1960 4110
100 305 500 1145 2490 4455
200 660 965 1690 3040 5240
500 1375 1775 2540 4040 6155
|
So, for example, it seems that there was a 10% chance that Double7 would
reach 1900 by 500 exp. The median time to reach 1900 is about 1145 exp, and
there was about a 10% chance that Double7 would not have reached 1900 even
after 2490 exp. If Double7 should be rated 1920, then the times would be
265, 445, 930, 2005, and 3310. On the other hand, she would get to 1900
slightly more slowly if she played only players of strength 1700: 330, 545,
1195, 2585, 4630.
By symmetry, one can also remain above one's true strength for as long a time.
|
|

|
3. Ratings Variations
|
|
Just from the luck of the dice, our ratings vary a lot from our playing
strength. Some of that comes from differences in playing style, say, when
one is tired, or if one plays overrated or underrated opponents. If one
ignores those effects, how much should one's rating vary?
The following tables give experimental evidence (from simulations) of how
much one's rating varies on GamesGrid assuming that one plays only
5-point matches against players of one's true strength. Note
that we assume there is a ramped period from 0 exp to 500 exp in which
ratings change more. These values were taken from samples of size 999, so
they are not exact. The values in the outer columns are less precise
(+−10 points) than those in the middle (+−3
points).
rating exp 1st 10th 50th 90th 99th stddev average
1500 500 1354 1415 1597 1584 1658 65.1 1499
1500 1000 1374 1436 1499 1565 1605 50.4 1499
1500 2500 1405 1446 1500 1554 1598 41.6 1500
1500 10000 1400 1445 1500 1554 1590 41.5 1500
1600 500 1440 1501 1587 1669 1731 63.5 1585
1700 500 1525 1580 1669 1752 1815 66.2 1668
1800 500 1595 1665 1747 1833 1900 65.8 1748
1900 500 1693 1743 1828 1922 1984 66.7 1831
2000 500 1758 1832 1914 1994 2055 62.2 1913
|
Interestingly, the ramped period increases the variance dramatically, but it
then decreases. The distribution after 10000 experience is more tightly
distributed about the true value than after 1000, and that is more tightly
distributed than after 500.
However, we can make a mathematical model for the limiting distribution that
we can solve. The probability density function of the stable distribution
satisfies the following differential equation, which comes from the fact
that as many players should increase past rating x as decrease past rating x
if the distribution is stable.

| pdf(x) |
represents the stable probability density function. |
| variance |
is the variance per experience, 16 p(1 − p) or 25 p(1 − p), where p is the probability of winning the match. |
| drift(x) |
is the restoring force per experience. |
| pdf'(x) |
is the derivative of pdf(x) with respect to x. |
This is satisfied when
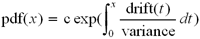
where the constant c is chosen so that
the total probability is 1. The result is a distribution which looks
similar to the Gaussian (normal) distribution, the classic bell curve, but
the tails are fatter.
With this solution, one can compute the percentiles of the stable
distribution on each of the servers considered. The following assumes that
one plays only players correctly rated one's true strength.
1st 10th 50th 90th 99th stddev
FIBS 1-point matches: -97.00 -53.43 0 +53.43 +97.00 41.69
FIBS 5-point matches: -97.16 -53.47 0 +53.47 +97.16 41.73
FIBS 25-point matches: -97.95 -53.71 0 +53.71 +97.16 41.98
GamesGrid 5-point: -95.51 -52.58 0 +52.58 +95.51 41.04
GameSite 2000 5-point: -108.68 -59.80 0 +59.80 +108.68 46.68
|
These are the limiting distributions. Over the very long run, a player on
FIBS playing only 5-point matches with correctly rated players
of equal
strength should spend 1% of the time with a rating more than 97.16 points
below the correct value. One is 200 points overrated just under a millionth
of the time—if you hear of someone honestly falling 200 rating points they
were probably overrated at the start and underrated afterwards.
The formulas for GamesGrid and for FIBS look different, but produce almost
exactly the same stable distributions. On the other hand, the formula for
GameSite 2000 only differs in that the total stakes for a match are 5
sqrt(n) rather than 4 sqrt(n). This means that the
half-life is smaller, but a string of victories has a greater effect on
one's rating, so the deviation from one's true rating is slightly larger.
Is the expected rating of someone of playing strength 1500 equal to 1500?
Oddly, no. What the rating system ensures is that the mode is 1500, i.e., it
is more likely that the player is rated between 1499 and 1501 than between
1549 and 1551. However, the median (50th percentile) and the average value
both depend on the strength of one's opponents, even with the assumption
that one's opponents are properly rated.
5-point matches on FIBS against opponents
1st 10th 50th 90th 99th average
of equal strength: -97.16 -53.47 0 +53.47 +97.16 0
100 points stronger: -97.87 -53.82 -0.19 +53.13 +96.45 -0.29
300 points stronger: -99.21 -54.48 -0.55 +52.48 +95.13 -0.82
|
While it is true that in this model one can increase one's average rating by
playing only weaker players, the effect is very small.
Another effect not captured by this model is that one's opponents are not
necessarily correctly rated. This is different from in chess, where almost
all tournament players say they are 150 points stronger than their ratings;
in backgammon there really are ratings swings. The direct effects are very
small. If players rated 300 points above one's strength are really either
200 points above or 400 points above with equal likelihood, then for the
purposes of playing 5-point matches it is as though they are
actually only
295 points stronger, so if one only plays people rated 300 points stronger
than one's rating, rather than averaging 1 point lower, one would average 4
points higher than one's true rating.
The assumption that players at a given rating are overrated or underrated
with equal probabilities is unreasonable, however. Someone rated 1850 might
have strength 1900 and a string of bad luck, or 1800 with good luck, but
there are more 1800 players than 1900 players, so someone rated 1850 is more
likely to be overrated than underrated. To what extent this is true is
outside the realm of mathematics, though conceivably a more detailed
analysis could model this, but by playing weaker players only when they are
overrated one can boost one's rating to the point that it is only a valid
indicator of how well one performs against overrated players, not most of
the population.
|
|

|
4. One's Maximum Rating
|
|
GamesGrid keeps track of each player's highest rating ever and makes this
information available in the player information. On other servers, we
suspect that players keep track of this data by themselves. How high should
this rating be? That depends on your experience level. If you play long
enough, you will get an astoundingly lucky streak.
The following tabulates the 10th percentile, 50th percentile, and 90th
percentile of the maximum rating of simulated players who start out with 0
experience points on GamesGrid and plays only 5-point matches.
Note that
the mathematical model may break down since people play differently when
they have had lucky streaks from when they have had unlucky streaks, and
their opponents may change, too.
rating exp 1st 10th 50th 90th 99th stddev average
1500 500 1500 1522 1588 1664 1724 53.9 1592
1500 1000 1500 1522 1590 1663 1742 54.2 1593
1500 2500 1509 1542 1592 1661 1712 46.2 1597
1500 10000 1548 1574 1609 1667 1728 37.5 1616
1600 500 1511 1565 1642 1726 1781 61.8 1645
1600 1000 1531 1580 1648 1722 1788 55.4 1650
1600 2500 1580 1617 1670 1732 1801 45.5 1673
1600 10000 1643 1664 1698 1741 1804 30.7 1701
1700 500 1565 1622 1710 1792 1865 64.2 1709
1700 1000 1609 1657 1728 1804 1873 56.4 1729
1700 2500 1671 1707 1755 1810 1871 41.0 1757
1700 10000 1741 1764 1794 1827 1875 25.7 1795
1800 500 1650 1704 1784 1874 1941 65.1 1787
1800 1000 1687 1737 1808 1881 1946 56.1 1808
1800 2500 1759 1798 1847 1899 1951 40.0 1849
1800 10000 1834 1858 1889 1923 1958 25.2 1890
1900 500 1709 1778 1860 1945 2016 66.9 1860
1900 1000 1769 1821 1893 1962 2033 55.8 1893
1900 2500 1852 1890 1938 1986 2032 37.2 1939
1900 10000 1930 1957 1990 2022 2055 26.0 1990
2000 500 1777 1848 1933 2026 2106 68.4 1936
2000 1000 1859 1913 1976 2045 2095 52.0 1977
2000 2500 1949 1983 2035 2081 2115 36.7 2033
2000 10000 2034 2059 2089 2124 2148 25.1 2090
|
There are many interesting phenomena which can be observed in the above table.
The top 90th and 99th percentiles don't change much for rating 1500 as one
increases the experience level. That is because the high ratings were almost
always achieved in the first 500 experience, when a winning streak has a
large effect. For example, in these simulations, only 1 of the top 100 out
of 999 maximum ratings for the experience levels of 1000 and 2500 were
achieved after 500 experience, and only 5 out of the top 100 for the
experience level of 10,000 were achieved after 500 experience. Eventually,
the swings after the ramped period will exceed the initial streaks, but
this will take a very, very long time if the streaks took one to over 150 points
above one's true rating. To a lesser extent, this occurs with stronger
players, but there is less time to achieve a very high rating before the
ramp expires, since part of the time is spent rising to the true rating.
Particularly for the stronger players and large experience levels, the range
of maximum ratings is relatively small compared to the range of ratings. At
2500 experience, the gap between the 10th and the 90th percentiles of the
maximum rating is about as large as the gap between those percentiles of the
current ratings, 100 points. However, at 10000 experience, the gap between
the 10th percentile and 90th percential of the maximum ratings is 60-65
points. For sufficiently large experience levels, the gap between the 1st
and 99th percentiles will be arbitrarily small, so the maximum rating will
be an extremely accurate indicator of the person's playing strength.
|
|

|
5. Estimating Playing Strength from Max Rating and Experience
|
|
Some players with ratings of 1750 on GamesGrid have highest ever ratings of
1760, and some have highest ever ratings of 1920. With which would you
prefer to play 100 games for $100 a point? One would expect that the second
player is stronger, and has had an unlucky streak, and the first has had a
lucky streak, but how can one estimate the true rating of each, assuming
that they have played consistently?
This is a subtle statistical issue, and the assumptions are not quite
accurate. However, we can use the table constructed above to try to answer
it within the model.
If after an experience of 10,000 the maximum rating of a player is 1860 and
they have been unlucky as they would be 1 time in 10, then their actual
playing strength is about 1800. If they have been lucky as they would be 1
time in 10, their actual playing strength is about 1740. That gap is smaller
than the difference between the 10th percentile and the 90th percentile of
the rating distributions.
Of course, to estimate one's playing strength, one should use both the
current rating and the maximum rating. However, for large experience levels,
one gets more information from the latter than the former. Even for players
of true strength 1500, after 10000 experience the standard deviation of the
maximum rating is smaller than the standard deviation of the rating.
Finally, what good does this do you? Perhaps nothing, but it might soothe
the irritation of a streak of bad luck, and remind you not to quit your day
job if you find yourself rated higher than Snowie.
|
|

|
Appendix: We are Right and They are Wrong
|
|
Ok, maybe they are right, too. Other people have written articles on the
ratings system, sometimes asking the same questions, and sometimes getting
different answers. We'd like to give pointers to some of these articles
contained in the rec.games.backgammon
archive and explain the differences. If you are interested in the
ratings system, it is worth looking at these other perspectives and
analyses.
|
|
|
Gary Wong's "Effect of
droppers on ratings."
This article introduces the idea of the half-life in one particular case and
applies it to the issue in the title. However, an arithmetic error and a
modelling error cause the half-life to be underestimated by a factor of 3.
|
|
|
Kevin Bastian's "Statistics."
This article does an empirical analysis of ratings variations from one
real-life history. The variations there are much smaller than those one
would expect from considering the stable distribution determined in section
3. The reason is that the history is very short. Two samples from the
ratings distribution that are one's rating before and after a
5-point match are highly correlated, and there can't be a large
difference between them. Even if the ratings are far from the player's true
average rating, they will be very close to their own average. This effect
biases the analysis, and his observed standard deviation (24) is much
smaller than the standard deviation of the stable distribution (42).
|
|
|
David desJardins' "No limit to ratings." and "Unbounded rating theorem."
These show that with probability one, your rating will exceed any given
level if you play long enough. That's true enough. How long will it take a
player whose strength is 1500 to exceed 2000? At a rate of one
5-point match per second, the player should be over 1900 one
second every 4 trillion years, but achieving 2000 happen
6 billion times less frequently. The expected time one waits
before achieving 1900 is longer than 4 trillion years by aproximately the
number of seconds one expects to stay above 1900 once it is achieved, which
is between 3.3 and 4.0.
|
|
|
Ed Rybak's "Ratings swing."
He reports the results of some simulations, including one similar to that of
section 2: How long does it take to bounce back from a 100
point rating drop? Note that for a distribution of this type, there
is a "fat tail." Our
reported median is smaller than his average value due to the small fraction
of times that the time to bounce back is very large; the average values in
our simulations agree with his.
|
|
|
Jim Williams' "Different
length matches."
From the actual results of tens of thousands of 1-point,
3-point, and 5-point matches he finds that the
correct lengths of these matches in the ratings formula should have been
1.6, 1.6, and 2.1 by the ratings formula, respectively, presumably by a
least-squares fit. Two conclusions: There is no more skill in a
3-point match than a 1-point
match, and longer matches have less skill than the ratings formula
indicates.
The problem with this analysis is that these come from real opponents,
rather than ideal opponents who always have their correct ratings. Because
of the natural variation, people will often be rated higher than stronger
opponents, or will have a large ratings difference against an opponent who
is only slightly stronger. These effects do not cancel out. The result is
that the effective match length will be underestimated by this method of
analysis even if the ratings formula is completely correct if one enters the
true ratings of the players.
Suppose player A is 60 points stronger than player B. A standard deviation
of about 40 says that the ratings are as varied as though half the time one
is 40 points overrated, and half the time one is 40 points underrated. If
this is the case with both players, then out of 4 matches between players A
and B, player A will be rated 140 points greater in one, 60 points greater
in two, and 20 points lower in one. That is a lot of variation. The
following table indicates the best (least-squares) fit to the effective
match length if the two play n-point matches and player A wins
exactly the
amount suggested by the FIBS ratings formula.
matchlength A's advantage effective length
7 60 1.97
5 60 1.40
3 60 0.84
1 60 0.28
7 100 4.08
5 100 2.90
3 100 1.73
1 100 0.58
7 200 6.21
5 200 4.39
3 200 2.61
1 200 0.86
7 400 6.99
5 400 4.94
3 400 2.93
1 400 0.96
|
Since the effective match length found by this method varies with the
difference in ratings, it is unclear what information one can get about the
relative skill levels needed to win matches of different lengths. However,
since it always underestimates the effective match length, this suggests
that 1-point matches may have slightly more skill than his reported
effective match length of 1.6 indicates.
|
|
|
William Hill's "Opponent's Strength."
He points out that two identical bots achieved ratings which differed by 150
points. The higher rated bot only played those with ratings under 1750, and
the lower-rated bot played only players with ratings over 1750. How can this
be reconciled with the statements at the end of section 3 which predict the
opposite effect?
I think the crucial factor here is that the player is a bot, and therefore
makes predictable errors that stronger human players can exploit
disproportionately well. That effect is not easy to model mathematically,
but if it is important then it does not invalidate the rating system for
human players. It might be that the ratings formula gives a good estimate
for the probability each player wins the first match that they play, but not
the 10th match in a row. Also, weaker players might be more likely to be
grossly overrated or to throw games to a bot. Still, it is an interesting
phenomenon.
|
|
|
Christopher Yep's "Possible Adjustments."
Among other interesting possibilities, he suggests adjusting the FIBS
formula so that the stakes for an n-point match are 2sqrt(n) rather than
4sqrt(n). The only difference between the FIBS formula and that of
GameSite 2000 is that FIBS uses 4 sqrt(n) and GS
uses 5 sqrt(n). It has been suggested that the bots should
have a smaller multiplier, perhaps as though the stakes were 0.5
sqrt(n) for it. What effect would these have?
Larger stakes decrease the half-life linearly, but increase the standard
deviation by a factor of approximately the square root. The standard
deviation of the stable distribution on GS 2000 is about
sqrt(5/4) times the standard deviation of the stable distribution on FIBS.
Decreasing the stakes would shrink the ratings variations, but lengthen the
half-life; one would
be misrated by less, but it would take longer to recover from a drop, or for
any improvements in skill to be reflected. If a bot were changed to move
only 1/10 as much as the other players on GS 2000, then the
standard deviation of its stable distribution would be 14.74 rather than
46.68.
|
|
|
FLMaster39's "Ratings
Variation."
This contains the information from experiments on the maximum ratings
similar to the ones tabulated in section 4. The main differences are that he
used longer histories, collected more data, and did not include a
ramped period but rather assumed that the ratings started at the correct
values. He also reports average values rather than several percentiles.
|
|
© 2001 by Douglas Zare and Adam Stocks.
Here is a Mathematica 4 notebook which shows how some of the computations in the article were done, and allows one to vary the parameters.

Return to
: Articles by Douglas Zare
: Backgammon Galore
|







![]()