Ideal Racing Positions
|
This original article is appearing here for the first time.
At the bottom is a link where you can download a table of ideal racing positions. |
What does it mean to say that a certain racing position is ideal? Position 1, for instance, the famous 3-5-7 position, is often described as the ideal starting position from which to begin a bear off in a race. Is Position 1 better than Position 2, another popular bear-off position? Is either one really ideal?
 |
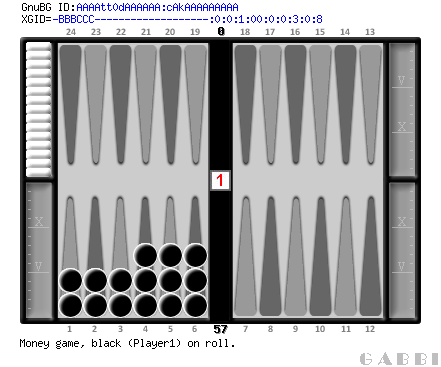
Position 1
The famous "3-5-7" position is ideal for racing. |
 |
Position 2
The best position for bearing off against opposition is not an ideal racing position. |
It should not be a surprise that Position 2 is the better racing position. Its pip count is 57, fully 22 pips better than Position 1. If you have to choose between Position 1 and Position 2, you should pick the latter. You'll win a lot more games. What may be a surprise, however, is that Position 1 is an ideal racing position, and Position 2 is not.
Computer programs have solved this problem completely. The average (i.e, mean) number of rolls remaining for any racing position has been calculated exactly. The results form what is called a one-sided bear-off database. Looking up Position 1 shows that it will require 10.5391 rolls on average to bear off all fifteen checkers. Position 2 requires only 8.13892 rolls.
The programs used to create one-sided bear-off databases make calculations based on the expected number of rolls remaining. It is common, however, to multiply the number of rolls by 8 and 1/6 (the average number of pips in a roll), to produce what is called the effective pip count (EPC). For any position, the effective pip count is always larger than the actual pip count. The difference is termed wastage. In practice, wastage occurs because some checkers will be borne off using numbers higher than necessary. Every time you use a 6 to bear off a checker from a lower point, you have “wasted” part of your roll. In Position 1, where the pip count is 79, the EPC is 86.0689. On average, slightly more than 7 pips will be wasted during the bear off.
So what makes Position 1 ideal? The answer is that it minimizes wastage. There is no other arrangement of checkers having a pip count of 79 that has less waste. We know this because a brute force search through all the thousands and even millions of positions in a one-sided bear-off database shows it to be true. Position 2, on the other hand, is not ideal. When the pip count is 57, and there are 15 checkers still in play, the ideal arrangement of checkers is given by Position 3. In Position 2, the EPC is 66.4679. For Position 3, it is 66.4081, a small, but nonetheless real improvement. Position 3 is an ideal racing position. Position 2 is not.
 |
Position 3
This position has the same pip count as Position 2. For a pip count of 57, with all checkers still in play, this is the ideal racing position. |
As players, we have very little control over the pip count. So long as we are not wasting pips, the dice determine what our pip counts will be. What we can control is wastage. By systematically choosing positions that are as close to ideal as possible, we can minimize the average number of rolls in a bear off.
To this end, I have produced the tables below. For each pip count and number of checkers still in play, they give the ideal racing position. With only a few exceptions, all of which occur when the checkers are piled onto the lower points, there is only one ideal position for any given pip count and number of checkers.
The first table, where the number of checkers is given as 0, lists the ideal racing positions for each pip count without regard to the number of checkers still in play. There might be only one checker, there might be fifteen, or there might be any number in between.
These tables are valid when all checkers are on or below the 11 point. Computations were made using IEC559 type double. Results were output in C++ using setprecision( 14 ), but it is likely that rounding and I/O conversion errors have corrupted the right-most digits.
Downloading the Tables in a Text File
Click below to open the tables. After they open, use File, Save to save them as a text file. You can view them in any text editor or word processor. If you are a Windows user, try Notepad. If the columns are jumbled, you'll need to change the font to one that is monospaced. Try Lucida Console or Courier New.
Downloading the Tables in a Spreadsheet File
Microsoft Excel users can download or open the tables in a spreadsheet by clicking the link below. In the spreadsheet version, all the tables have been merged into one Excel table. After opening the file in Excel, click the triangle next to the column name "Checkers" to select how many checkers should be displayed.
Copyright 2011 Michael J. Mannon
All rights reserved.
Last updated: 28 June 2011