Analysis of a Bluffing Game Involving a Doubling Cube

   In backgammon the doubling cube can be used to raise the stakes of a game. Initially the cube is at 1 and is “in the center” with either player “having access” to it.  On a player’s turn he may before rolling double the stakes of the game. The opponent may either decline and lose the current stake or accept and play on with the stake of the game being doubled.  Either player may make an initial double but when a double is accepted the accepting player now “owns” the cube.  That player could later redouble to 4 with the opponent either declining the cube and losing the current value of 2 or playing on with the stake of the game doubled. There may be later redoubles to higher levels.

  The following game is a generalization of a position from a backgammon variation shown to me by Malcolm Davis. The variation is that the player may roll first and observe the result of the dice without the opponent seeing the roll, and then decide on doubling or not.  Malcolm’s position was a “last roll” situation in which the outcome of the game is entirely decided on the very next roll. There will then be no further cubing which simplifies the analysis.

    Suppose that A and B are gambling 1 unit on the result of a coin flip.  The coin lands heads with a probability  known to both players.  If the coin lands as a head then A wins the bet.  There is a stakes doubling mechanism in that A observes the result and may then offer to double the stake of the bet to 2. B must then either decline and lose 1 unit or accept and have the stake of the bet then be 2. Note that A may bluff.  If the coin has landed as a tail A could still win the bet by doubling if B declines the cube.

     If the coin lands heads with probability of at least .75 then dominant strategies exist. Player A could simply not even look at the roll and just double every time. If player B takes then the expected gain to A is   for .  If player B just passes every time the expected gain to A is +1.  Thus A should always double and B should always pass.

     What if  ? Randomized strategies may then be best.

     Define probability that player A bluffs by doubling when the coin has landed as a tail.

 probability that player B takes an offered double.

   As a function of , , and  the expected value of the game to player A can be found by considering various cases and adding the results.

     With probability  the coin lands as a head. Player A wins the bet. He clearly should cube and will win 1 if B declines and 2 if  B accepts.  The coin landing as heads thus contributes

to the expected payoff to player A.

      With probability  the coin lands as a tail. If player A decides to not bluff he loses $1.

If player A decides to bluff then he wins 1 if B declines the cube and loses 2 if B accepts the cube.  The coin landing as a tail thus contributes

 to the expected payoff to player A.

        Adding, multiplying, and simplifying results in:

Value of game to A

Suppose that player B has announced a value for . What value should player A choose for?

          We can rewrite the expected value equation as

The value of  being positive or negative decides what value of  maximizes this function.  Algebraic manipulation shows that  is equivalent to   leading to the following result:

The value of d that maximizes  is given by

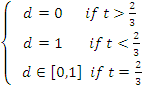
  One way to look at this is that if player B is taking often then A should not attempt to bluff. A gains instead from all the times that A wins 2 instead of 1 when the coin lands as a head.

   Suppose that is changed from   to a value  larger than  .  We may without loss assume that player A had been choosing   and we see that player A gains equity of

.

     Suppose that is changed from   to a value  smaller than  .  We may without loss assume that player A had been choosing   and we see that player A gains equity of

.  For   that equity gain is positive.

     We conclude that the minmax value for player B is to choose   if   and to choose

 otherwise.

    Now let’s look at the minmax strategy for player A.  Supposing that player A has announced a value for  we can rewrite the expected value equation as

       What value should player choose B to minimize this expression?

        The key value here is  being positive or negative or zero.  Noting that

 is equivalent to   we have that the value of  which minimizes the expectation to player A is given by:

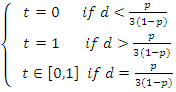
                One way to look at these results is that if player A seldom bluffs then B should always drop. The doubles are probably coming only when the coin has landed as a head.

             A similar analysis as that done in the previous case shows that the minmax strategy for player A is to choose  if .  Otherwise choose .

Note that this is  the ratio of favorable to unfavorable coin flips.