Effective Pip Count
|
This article originally appeared in the November 2000 issue of Flint Area BackgammoNews. It is republished here with the kind permission of Walter Trice and Carol Joy Cole. |
Even the simplest backgammon positions have their little secrets. Case in point:
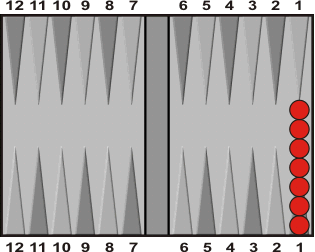
Depending on the dice, it takes 2, 3, or 4 rolls to bear off 7 men from the ace-point. Simple multiplication of probabilities shows that the chance of bearing off in 2 rolls is 1/36 and that the chance that 4 will be needed is 125/216. What remains—(1 - 1/36 - 125/216)—is the probability of bearing off in 3 rolls. From these figures, one can calculate the average number of rolls required, and it turns out to be 3.5509259259.
3.5509259259. Hmm. Pretty dull. Multiply it by 49/6, though, and something interesting happens. You get 28.999.
Could it be just a coincidence that this process produces a number that is almost an integer? Well, maybe. But if you do the same thing for a 13-checker stack, the result is even more interesting: 50.000004.
When I encountered these numbers 11 years ago, the first thing I had to do was pop my eyeballs back into their sockets. Then I went to work on an algebraic formula for the sequence, including the "error" term. I sent it off to Danny Kleinman, whom I figured was the only other person on the planet who would find the thing as fascinating as I did. Danny worked out a simpler derivation than mine and wrote it up in an article ("Walter's Wonderful Formula") that he included in his next book (... But Only The Hogs Win Backgammons).
You may be wondering exactly why 49/6 entered the picture. 49/6 is the average number of pips in one roll of the dice. If we didn't get to play our doubles twice in backgammon, the average roll would be 7, just as it is in craps. But doubles gives us two bangs for the buck. Since doubles occurs once in 6 rolls, we average 7 bangs for 6 bucks, or 7/6 bangs per buck. Since the average bang is still 7 pips, the average roll is 7/6 x 7 pips, or 49/6. Thus, when we multiply some number of rolls by 49/6, we are converting a "roll count" to a kind of pip count.
Relationships like the one between the 4-roll position and the number 29 needed a name, and I decided to call 29 the Effective Pip Count, or EPC, of the 4-roll position.
All pure ace-stack positions have EPCs that are very close to whole numbers.
The general formula is as follows:
| Rule 1: For an N-roll position, the EPC is 7N + 1. |
For a 1-roll position consisting of 1 or 2 men on the ace-point, you get 7 x 1 + 1 = 8. The "real" answer is greater by 1/6 of a pip. But every time you go out one more roll, the error in the formula decreases by a factor of 6, so it quickly becomes insignificant. For a 7-roll position the formula gives 7 x 7 + 1 = 50, and as we have seen, the error is only 4-millionths of a pip.
Lured by the possibility that other classes of positions might have EPCs that could be calculated just as easily, I began looking at home board bear-off positions, multiplying the average number of rolls it took to bear them off by 49/6. The next rule to emerge was more approximate than the neat 7N + 1 rule, but it had a broad range of applicability. In a nutshell, Rule 2 was as follows:
| Rule 2: Nice positions waste 7 pips. |
A "nice" position consists of a smoothish cluster of checkers on the 4, 5 and 6 points. For a nice position, you get the EPC as follows: count pips the normal way, and then add 7.
Rules 1 and 2 lead to a very efficient method of gauging cube action in roll-vs.-pip positions. The method is best illustrated by a position I call "Prop 57."
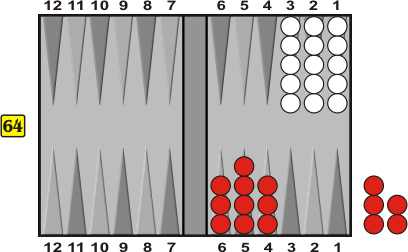
Which side do you think stands better here? A few years back, players tended to grossly overestimate the value of Red's having already borne off five men. I would offer to play backgammon from this position, rolling to see who goes first, cube in the middle, for small stakes—just to make it interesting. After a few dozen points had dribbled away, my opponents usually decided that they were on the wrong side. No problem, I'd say, turning the board around ... Oddly enough, switching sides didn't seem to make a difference!
Red is slightly better, but unless both sides handle the cube skillfully, the positions are, for all practical purposes, equal. White's position is close to an 8-roll ace-point stack, so Rule (1) says that his EPC is 57. Red has a nice position with a pip-count of 50, so Rule (2) says that his EPC is also 57. As the game progresses, most of the time Red stays semi-nice and White stays crunched, so the two formulas keep working.
The Prop 57 player's edge comes from his being able to handle the cube decisions quickly, effortlessly, and with above-average accuracy. One set of guidelines works well for pip-vs.-roll positions and for roll-vs.-pip positions, if both sides are converted to EPC. Here's how it goes. Start with the "number of rolls" for the position of the player on shake, and subtract 3. This is the maximum deficit in EPC with which the trailer can take a double. If the trailer is within 1 pip of his point of last take, the leader can redouble. Within 2 pips, it is an initial double.
Suppose, for example, that in Prop 57 White wins the opening shake, taking off two men, and then Red rolls his worst number, which is 2-1. Now White is in a 7-roll position with an EPC of 7 x 7 + 1 = 50, and Red has reduced his EPC from 57 to 54. 7 minus 3 is 4, so Red has a bare take, down 4 = 54 - 50. If, instead, Red had rolled 3-1 or 1-1, he would be down 3, and 1 pip better than his point of last take: (re)double/take. If Red had rolled 3-2 or 4-1, the position would be an initial double for White, but not a redouble.
When Red wins the opening shake, the picture is a bit different. If Red rolls 6-5 and White fails to roll doubles, then White should drop Red's cube, though it's close. You might think that this sequence would mirror the [White: any roll / Red: 2-1] case, since 2-1 is 4 pips smaller than an average non-double and 6-5 is 4 pips larger, but there are three extra factors working in Red's favor. First, after 6-5, Red is not in a "7-roll" position: an EPC of 46 is a 63/7-roll position. Second, when Red rolls something that lets him take off checkers without being forced to dump any onto his three low points, his position becomes even "nicer" and his wastage diminishes by a small fraction of a pip. And finally, the two sides aren't really equal to start with. Red's edge in the initial position is equivalent to 3/10 of a pip.
I don't use Effective Pip Count methods for every racing cube decision. Most of the time the plain vanilla pip count is all you need to know. When in doubt, I'll use Jeff Ward's adjusted pip count. I reserve EPC for these asymmetrical roll-vs.-pip positions and for certain peculiar types of races that emerge after someone gets hit in a contact endgame.
In the world of EPCs, a few reference positions go a long way. One reference position deserves its own rule.
| Rule 3: The flat position wastes 10 pips. |
The flat position is a simple closed board, two checkers on each point. If a position is smooth, flattish and top-heavy, it will always waste fewer than 10 pips and more than 7.
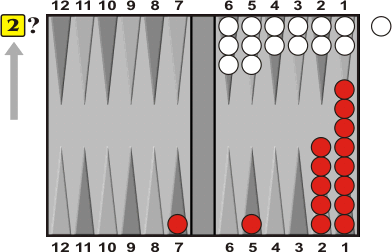 |
Towpath Tournament September 2000
15-point Finals:
White has borne
Red on roll. |
In the position that arose in my match with Mike Friedman at the Towpath Inn Tournament, my over-the-board guess for White's wastage was 9.5. Undoubtedly I had seen the exact position—flat with spares on the 5 and 6—at some time on a computer screen, along with its EPC and wastage, but I had never committed it to memory. So it's a coincidence that the real answer differs from 9.5 by only a hundredth of a pip. White's EPC, then, is 53 (his literal pip count) plus 9.5 for a total of 62.5.
Red has 15 checkers with 16 crossovers. If he always gets 4 crossovers from his doubles, and 2 crossovers from his non-doubles, then he'll have played out an 8-roll position. But a single miss costs a full roll. Over the board I again made an educated guess, and estimated that Red was 2 pips worse than an 8-roll position. So my EPC estimates were 59 for Red and 62.5 for White. Since the "roll-vs.-pip" guidelines said I could take being down 5, I was quite comfortable with my decision to take, and I didn't bother to get into the tedious counting of two-roll miss sequences that would have been necessary for a more exact calculation of Red's EPC. It was obvious enough that Red had a goodly number of ways to miss by rolling a 3 or a 4 on his second shake.
A closer (and computer-assisted) look at the position reveals an interesting nuance. Red's EPC turns out to be 59.6. This puts him at about a 3-pip lead, and the pip-vs.-roll rules suggest that Red might have an initial double, but not a redouble. But a Snowie rollout indicates that in fact Red does have a money redouble. How come? The reason is that the Towpath position is not really a pip-vs.-roll position. White is 2.5 pips away from "nice," and higher wastage also implies lower variance. "Lower variance" means less joker-potential. Less joker-potential means that it is harder to catch up if you are behind, which magnifies the significance of your opponent's lead.
I felt challenged by the Snowie result to find a minimal modification of White's position that would vindicate the old guidelines. Here it is:
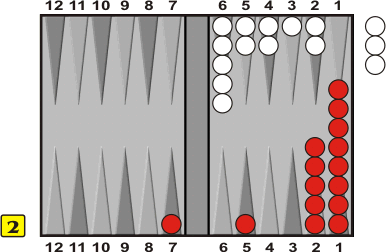
White's position may not look as pretty as the Towpath position, but it is in fact almost 2 pips nicer, as a result of his having 3 fewer checkers on the low points, and none on the ace. This almost makes up for the fact that White's pip count is now 55 instead of 53; his EPC is 62.58 instead of 62.51. Although White's higher EPC results in a numerically greater lead for Red, the modified position is indeed not a redouble.
| Walter Trice is an expert player in the Boston area, and statistician/editor of the New England Backgammon Club. His backgammon software creations include the Bearoff QuizMaster, and the Match Equity Generator (MEG3), which supplements the book he co-authored with Jake Jacobs: Can a Fish Taste Twice as Good? Walter is a regular columnist at GammonVillage. His latest book is Backgammon Boot Camp. |
Last updated: June 2004