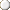|
Backgammon in one form or another has been with mankind for over 5000 years. Unlike games of pure skill such as Go or Chess, Backgammon involves both skill and the randomness of the dice. In life, our basic principles and ability to adapt to whatever situation we find we are up against determine how successful we are. The same goes for backgammon. Without basic theory we are lost as to what we are trying to do. Without flexibility and adaptability, we cannot efficiently react to the randomness of the dice.
The purpose of this series of articles is to provide a very basic framework for understanding the game of backgammon. Once the basic principles and goals are understood, we learn to assess our game and define our goals. We can then intelligently develop a strategy to achieve them. Once we have the basic strategic framework, we then spend years refining and perfecting our tactical styles based on study, the play of masters, and our own experience.
"If I have a six sided dice, and roll a 2 one hundred times in a row, what is my chance of rolling a 2 this time?" The answer depends on two things—do dice have memory and can you hold your mouth just right when you roll. Unless the dice are loaded, no matter what you do, wish or calculate, the chance of rolling a 2 is still 1/6. They do not know what they were last roll, what you need them to be this roll, or what your opponent wants them to be. They don't care, nor can they be bribed, threatened or pleaded with. They are like cats.
With two dice, there are only 36 possible combinations of rolls (6 × 6). Of those 36 possibilities, there are 6 doubles (1-1, 2-2, 3-3, 4-4, 5-5, and 6-6) so your chances of rolling a double are 6/36 or 1/6.

The 36 different combinations of dice. Six combinations are doubles.
Since you have a 1/6 chance of rolling a double, you must have a 5/6 chance to roll a non-double. The chance of rolling a particular double, like 6-6, is 1/36 because there is only one way to roll it. Non-doubles have a 2/36 chance because there are two ways to roll the same number: 2-5 and 5-2 for example.
Another key concept is the ability to understand how many rolls out of 36 will allow you to do something you want to do. Suppose you have a checker on the bar and your opponent has all his home points blocked except for his 5 point. To get back in this turn, you have to roll a 5. How many chances out of 36 possible rolls include a 5?
|
| |
How many rolls out of 36 allow red to enter from the bar?
|
Well, obviously if you roll a 5 on one dice, you can roll any of 6 numbers on the other dice and still have a 5—that is 6 different combinations. By the same token, if you have a 5 on the other dice, you can roll any of 6 numbers on the first. That is 12 different possibilities. The only flaw with this argument is that you have to make sure that you don't count the same roll more than once. Note that a roll of 5-5 can only be made once out of 36, like any double. Since 5-5 is being counted twice in the discussion above, we need to change our 12 total rolls to 11. Using the same logic, we find the chance of rolling any designated number from 1 to 6 with two dice is 11/36 rolls.
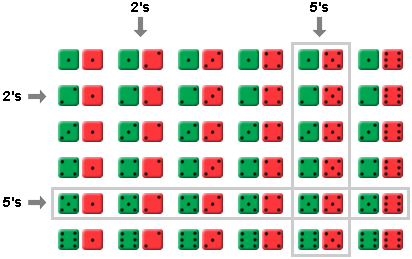
The 11 different ways you can roll a 5. Be careful not to count 5-5 twice.
To continue, what if instead of just the 5 point being open in the example above, both the 5 and the 2 point were open? If we applied the same logic, remembering to not double count doubles and paying attention to rolls like 5-2 and 2-5 we find that our first impression of 24 rolls (recall 1 seemed to have 12 possible rolls, so 2 must seem to have 24) needs to be adjusted to 20. We see how to calculate it, now we simply memorize the numbers. Any 1 number is 11 rolls of 36, any 2 are 20, any 3 are 27, any 4 are 32, and any 5 are 35.
Another adjustment needs to be made before we have the final word in calculating how many rolls out of 36 let us do something we want to do. Consider this example: Say there are three checkers on the board. You have one on your 24 point, and your opponent has one checker on each 23 and 18 point (1 and 6 checkers away from your man). It is your roll, how many shots hit each checker, how many hit both?
|
| |
How many ways can red hit one of white's blots? How many ways can red hit both blots?
|
The simple answer is easy, 11 rolls contain a 1, 11 rolls contain a 6 and 20 rolls contain either a 1 or a 6. But that is not the whole story. While 11 rolls do contain a 1 and hit the man on the 23 point, not only do 11 rolls contain a 6 to hit the man on the 18 point but so do 5-1, 4-2, 3-3 and 2-2 for a total of 17 possible rolls. To continue, we must add a couple of these rolls to our 20 rolls that hit either the man on the 23 or the man on the 18—specifically 4-2, 3-3 and 2-2 because the 5-1 is already counted in the 11 rolls that contain a 1. This gives us a total of 24 rolls that hit the man on the 23 or the man on the 18. Only a 5-1 hits both, and that is only 2 rolls out of 36.
What about when we have to roll a number greater than 6? Take the above example with our man on the 24 point, remove the enemy checker on the 23 and move the checker on the 18 back to the 17 point. That checker is now 7 pips away from our man on the 24. We can hit it with a 6-1, 5-2 and 4-3 which is 6 rolls. No doubles will hit it.
If we moved it back one more to the 16 point (8 away from our man), we could hit with 6-2, 5-3, 4-4 and 2-2, also 6 rolls. On the 15 point (9 away) we have 6-3, 5-4, and 3-3, 5 rolls of 36.
Why is this information important for us to know? Because like in life, we take risks in backgammon in order to succeed. We need to be able to calculate or at least estimate those risks in order to find the best play and the best balance of safety vs aggression in our tactical play. If I wish to slot a key point, how likely is my opponent to hit that blot? How many rolls out of 36 do I have to complete my prime or hit a shot? If I can't do something good this roll, how can I set up my checkers to give me the greatest chance to do something next roll? If I have to expose a weakness, how can I make it painful for my opponent to exploit it (if he hits me, can I re-enter and hit him back for example).
A more important aspect, however, may be when we are playing with the cube. A basic premise of the cube is that you can double when you have at least a 50% chance to win (or 18 winning rolls out of 36 if you are in a last roll situation) and your opponent can take when he has at least a 25% to win (or 9 winning rolls of 36). Let's see an example:
You are on the 1 and 4 point, your opponent has 2 on his one point. You are on the roll, if you bring both in you win, if you don't you lose. This is a last roll situation. How many rolls win the game for you? Can you double (do you have at least 18) and can your opponent take your double (do you have at least 9 rolls that don't take both men off)?

|
| |
Should red double?
Can white take?
|
This can be directly calculated over the board in one of two ways. You can calculate your winning rolls or you can calculate your losing rolls and subtract that number from 36. First the winning rolls—any 6, any 5 and any 4 win, plus 2-2, and 3-3—29 rolls. How about the losing rolls? 1-1 is the only double, 2-1, 3-1, 3-2 or 7 rolls. You double, your opponent passes. If you fail to double, you give your opponent 7 out of 36 chances to win a game you could have ended with the cube on your turn.
Another way to calculate your winning chances is to multiply probabilities. Consider a two roll situation where you and your opponent both have 4 men on your one points and it is your roll. To win you need to have one of two things happen, you have to roll a double or you must roll a non double and your opponent must roll a non double. Your chance of rolling any double is 1/6 so you win outright on 6 rolls. Add to this the probability of rolling a non double and your opponent rolling a non double which is 5/6 × 5/6 or 25 rolls of 36. Your total winning chances are 6 + 25 or 31 of 36 rolls. Your opponent wins only if you roll a non double and he rolls a double. The probability of this is non double (5/6) × double (1/6) or 5/36. He has 5 rolls out of 36 to win. The answer is the same in both cases. Double and pass.
Finally, what about more complicated positions?

|
| |
Should red double?
Can white take?
|
Red is on the roll and considers a double. Does red have a double and does white have a take? This is not a two roll position as all doubles do not take off 4 men and all nondoubles do not take off 2 men.
Just by glancing at the position we see red's winning chances are greater than 50%—he wins outright on doubles greater than 3-3 (4 rolls) and of the other 32 rolls, white must roll a double other than 1-1 to win, so red picks up another 33 × 31/36 games for 28.4, for total winning chances of 32.4. But there is a complication if Red rolls a lone 2 (2-2 really acts like a non-double and takes off 2 checkers) because, in these games, white can roll a non-double and take off 2 checkers, red can roll and fail to win, then white can roll again and win. So in our first glance red clearly has a double, the question is can white get up to 9 of 36 winning chances? Maybe, but let's work it out exactly.
White can win the game in the following circumstances:
Variation 1: Red rolls a 2 except for 2-2.
This results in a position like this:
|
If Red rolls 2-1
|
If red rolls 2-3, 2-4, 2-5, or 2-6
|
Of the 8 rolls where Red ends up with 3 checkers on the 1 point, White will win outright with 5 sets of doubles (1-1 leaves a man on the 2 point). This gives him 5/36 of 8 games or 1.11 games. Of the remaining 31 rolls White will roll again and take off his last 2 checkers unless Red rolls doubles and takes off all three remaining checkers. This gives another 8 x 31/36 x30/36 or 5.74 games for a total of 6.85 games in this variation.
In the case of red rolling 2-1, White will roll and win 5/36 games outright with doubles greater than 1-1 as above. This gives him 5/36 of those 2 games or 0.277. Red then rolls nondoubles and white wins for another 2 × 31/36 × 30/36 or 1.44 games.
To total everything up, if red rolls a non-double 2, white gets 1.11 + 5.74 + 0.277 + 1.44 = 8.57 games.
Variation 2: Red does not win with doubles but white does.
Since Red wins with 3-3, 4-4, 5-5 or 6-6 (4 rolls) and white wins with 2-2, 3-3, 4-4, 5-5 or 6-6 (5 rolls) this works out to 32/36 × 5/36 = 0.12 games.
(Running total, White is up to 8.69.)
Variation 3: Red takes a man off from both the 1 and 3 points and still loses.
Red rolls 6-1, 5-1, 4-1 or 3-1 (8 rolls). White the rolls doubles and wins (5 rolls). 8 × 5/36 = 0.89 games. White takes off 2, red rolls 2-1, white rolls and wins. 31/36 × 2/36 = 0.05.
So white's total winning chances are: 8.69 + 0.89 + 0.05 = 9.63. Yes, it is a double/take.
Gnu rollout shows:
| Double/Take | 0.502 |
| Double/Pass | 1.000 (+0.498) |
| No Double | 0.275 (−0.277) |
Why, the alert reader may ask, does not offering a double drop red's equity from 0.502 to 0.275? After all, red is nearly at 75% to win the game. Why does red take such a hit by not doubling? The answer lies in the concept of cube ownership and equity, something we will discuss more in the next article but food for thought now.
Recall from the above discussion that white becomes a very heavy favorite in the 10 rolls where red pops out a 2. If the cube is not turned by red, white will turn it and red must drop, losing all 10 games. Granted, this will happen even if white accepts the double to start with, but the extra points red will win on the other 26 games with the cube at 2 more than make up for the 20 points red loses dropping white's redouble.
Here are some fast and dirty numbers. Look back in the article and see where they come from:
Red Doubles and White Takes
Red does not roll a 2 (26 rolls):
Red wins all but the less than one game accounted for in variations 2 and 3, say 25 games for 50 points.
Red rolls a 2 (10 rolls):
Give them all to white at 2 pts each or 20 points.
Red nets about 30 points in 36 possible rolls or about 0.83 points a game on average.
| |
Red Does Not Double
Red does not roll a 2 (26 rolls):
Red wins 25 points as above.
Red rolls a 2 (10 rolls):
White doubles and Red correctly drops. White gets 10 points.
Red nets about 15 points over 36 possible rolls or about 0.42 points per game on average.
|
Not paying attention to turn the cube when you should will cost you in the long run.
In the next article of this series, we are off to the races. We will look at the racing game plan, how to evaluate a position in long and short races, how to handle the cube and the concept of cube ownership. We will also introduce the term equity.
To build on what we have learned so far, here is a position to consider:

|
| |
With the cube in the center, does red have an initial double and white a take?
|
|
|

|
| |
With the cube on 2 and owned by red, does red have a redouble and white a take?
|
|
Continue to Part 3
|


![]()