Examining the weekly club and the monthly
team score sheets, I notice a lot of matches that go into the Crawford
game from a tied score of 2-away, 2-away. The theory is that, between
two strong players, the 2-away, 2-away game should be the last. This is
because it always pays the leader to offer the cube and play for the match,
however slim his lead, and as one of the players will always be the leader,
the game should always be doubled. Thus it should only go to Crawford
if the leader erred and missed his market, by waiting unnecessarily.
Winning a single point, the leader's match-winning
chance (at 1-away, 2-away) is 70%. So if his game winning probability
is p (ignoring gammons), his match winning equity is:
0.7p + 0.3(1 − p) = 0.3 + 0.4p
If he cubes, his match winning probability is exactly that
of this game, p. Now p > 0.3 + 0.4p when p > 50%;
i.e., whenever the player has any lead at all.
A lot of players know this, but they only don't
wish to double prematurely with a small lead, in case their fortunes
are reversed and they find themselves trailing. As the theory goes this
is an unnecessary risk, as a knowledgeable opponent will not let you get
below your drop point, so the only risk you run is of losing your market.
At this score this is much higher than usual, as your opponent's drop
point is 30%, compared to an early match or money game where it could
be as low as 20% due to recube vig.
So while most of us are wondering just
how small an advantage is enough to double, the fact is, that it can sometimes
pay to cube even when you are trailing in the face of even a smallish
market loser! Take the following bearoff position as an example.
 |
|
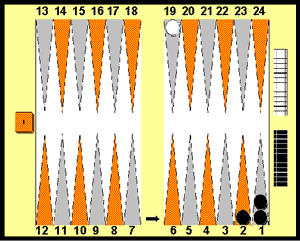
Position 1:
21 point match
Black 19, White 19
Black on roll. Cube action?
|
If black does not cube his chances are
as follows: 1/6th of the time he will roll a double and go into the lead
(20 to 19) with a 70% match equity. On those 5/6th of the time that he fails,
white should cube and black will have to drop, leaving him trailing (19 to 20)
with a 30% match equity. (With white on roll and only 1 man left, black
actually has a 25% chance of winning, but as his drop point at this score
is 30% he cannot take). Combined, this gives black a total match equity,
before rolling, of 36.7%.
If black does cube, however, 1/6th of the
time he will win the match. If he fails he still has a 25% chance of winning
as there are nine rolls which fail to get white off. White cannot cash
once black has doubled, as the cube will be dead, so in 5/6th × 1/4
cases black will still win. This combined probability is 37.5% which is
higher than his uncubed chances.
Admittedly the above position is unlikely
to come up very often, if at all, in a player's lifetime, as the score
has to be 2-away, 2-away and the cube unturned as well. However it does
appear in different guises throughout the game, such as in the following
position. Assume again that the score is 19-all playing to 21, black on
roll:
 |
|
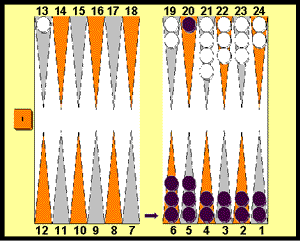
Position 2:
21 point match
Black 19, White 19
Black on roll. Cube action?
|
Here again black is trailing; in Position
1 he had to roll one of six doubles to win, here black has six indirect
shots to do the same. If black failed in Position 1 he would have to drop
the inevitable cube from white.
In Position 2 his racing chances are slightly
better than 25% which still means a cash because of his 30% drop point.
(If he does not hit or clear the white checker on this roll black does
have a few chances of a second shot, but most of this advantage is lost
in burying his checkers, so his overall chance if he rolls and fails is
just off 28.5%). As his chances are even better than in Position 1, black
knows he is better off cubing without having to do a lot of fancy calculations.
These are black's probabilities. If he
fails to cube, then, just as in Position 1, he has a 1/6th chance to hit
and win, or he will be cubed out for an overall match winning probability
of 36.7%. If he does cube , 1/6th of the time he will win the match and
5/6th of the time he will be left with a 28.5% survival chance for an overall
41% match winning chance.
So, even though he trails with a 41% game
winning chance, it pays black to cube and make that his match winning
probability, a big improvement over his uncubed 36.7%.
