
|
This article was previously published in the Chicago Point (visit their web site!),
Issue #52, November 1992. It was made available on the Internet in 1997 by
Kate McCollough |

Jack Kissane, backgammon master from Albany, New York, is known in many chouette circles as the fastest pip counter in the world. In a June 1989 Chicago Point interview, Kissane claimed that he can count almost any backgammon position within five seconds.
For the first time anywhere, Jack Kissane shares his counting techniques with the backgammon community. Enjoy!
Pip counting. How do you view it? An annoyance? A necessity? Just part of the game? Some backgammon players can't or won't be bothered doing a pip count. Others use the count as a crutch, basing far too many checker moves on it. After a hard day of match play or during an all-night chouette, pip counting can be sheer torture, draining our limited supply of "thinking" energy. However, once or twice a game, knowing the count is critical for making the right checker play or, more importantly, the correct cube decision.
Over the years, I have developed a system of pip counting that significantly reduces the amount of time needed to count a position. I call it Cluster Counting. Hopefully, this fairly simple system will help you minimize the drudgery of pip counting and thus increase your enjoyment of the game.
Basically, Cluster Counting involves the mental shifting of checkers to form patterns of Reference Positions (RP) whose pip totals end in zero (with two notable exceptions) for quick, easy and accurate addition. Here are my seven basic reference Positions:
| Reference Position #1: 5-Prime. | |
|---|---|
| 5-Primes. Multiply the midpoint of any 5-Prime by 10 and you have just counted a cluster of ten checkers. This position shows a 5-Prime from the 4-point to the 8-point. | |
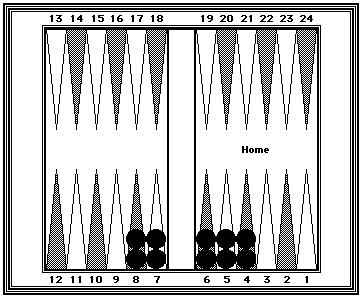 |
Black=60. The 6-point is the midpoint and the count for these ten checkers = 60 pips (6 x 10.) This is so because 5s and 7s average out to 6s, and 4s and 8s also average out to 6s. |
| Reference Position #2: Closed Board. | |
|---|---|
 |
Black=42. This is just a 5-Prime around the 4-point plus two checkers on the ace point. |
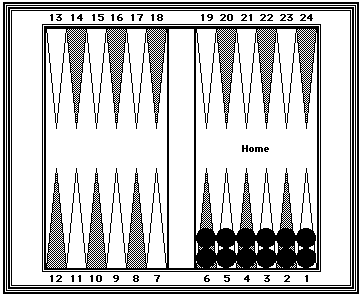
| Reference Position #3: | |
|---|---|
 |
Black=70 Five checkers each on the 6- and 8-points. |
| Reference Position #4: | |
|---|---|
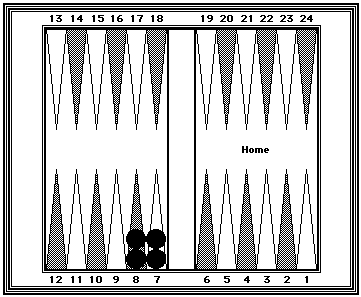 |
Black=30 Two checkers each on the 7- and 8-points. |
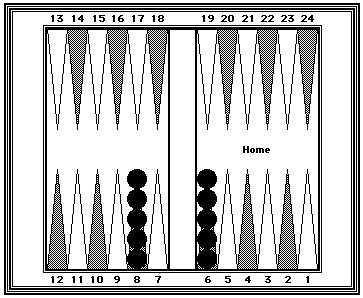
| Reference Position #5: | |
|---|---|
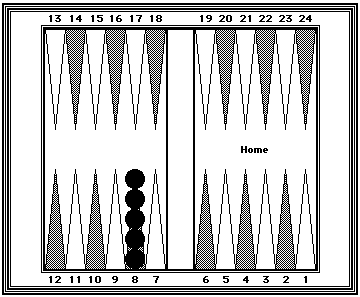 |
Black=40 Five checkers on the 8-point. |
| Reference Position #6: | |
|---|---|
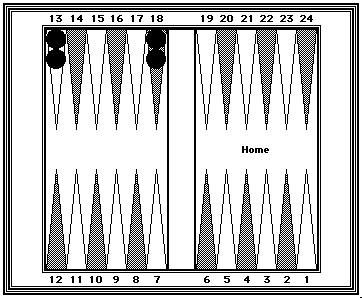 |
Black=62 Two checkers each on the midpoint and opponent's bar point. |
| Reference Position #7: | |
|---|---|
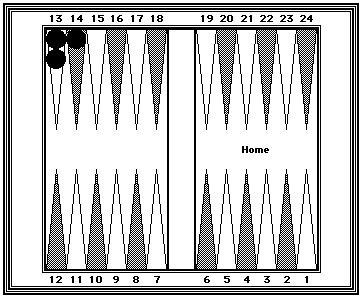 |
Black=40 Two checkers on the midpoint and one on the 14 point. |
These seven Reference Positions combined with Key Points and Mirrors are the backbone of Cluster Counting.
The two Key Points most often used are the 5-point and the 20-point (opponent's 5-point.) The 10-, 13- and 15-points are also quite valuable.
| Position 8: Making use of the 5-point as a KEY POINT. | |
|---|---|
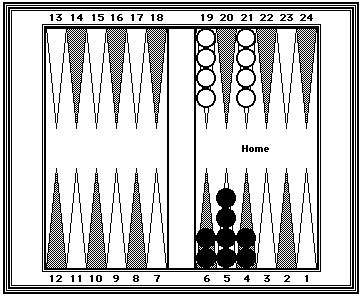 |
Black = 40 White = 40 This position shows two examples of counting a cluster of eight checkers all at once as if they were eight 5s = 40. |
| Position 9: Making use of the 20-point (opponent's 5-point) as a KEY POINT. | |
|---|---|
| The 20-point (opponent's 5-point) is the most useful Key Point. All checkers in your opponent's home board should be counted as 20 plus the pips required to get to the 20-point. | |
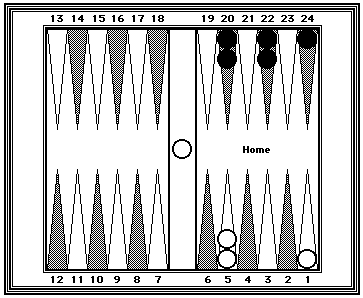 |
Black = 108 White = 89 Black's count is 108 which can be visualized as five 20s + 4 (two each from the 22-point to the 20-point) + 4 (one from 24-point to 20 point). White's count is 89, visualized as four 20s + 4 + 5 (for the checker on the bar). |
Mirrors are another important counting tool. Any point on the board plus its mirror-opposite point equals 25. For example, the 5-point + 20-point, the 1-point + 24-point, and the 12-point + 13-point all total 25 pips. It follows that any cluster of 4 checkers in mirror positions total 50. See Positions 10 and 11:
| Position 10: Using MIRRORS to count a cluster of four checkers. | |
|---|---|
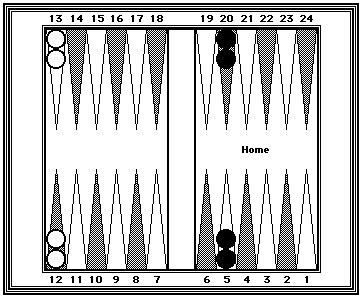 |
Black = 50. White = 50. (13 + 12 = 25) x 2 = 50. (20 + 5 = 25) x 2 = 50. |
| Position 11: Using MIRRORS to count a cluster of four checkers. | |
|---|---|
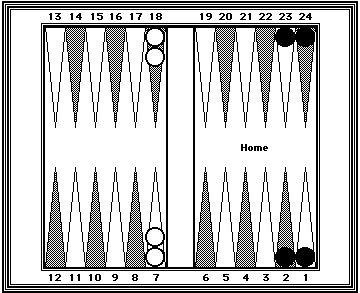 |
Black = 50. White = 50. (18 + 7 = 25) x 2 = 50. (23 + 2 = 25) + (24 + 1 = 25) = 50 |
OK! It would be nice if every time you needed a pip count, the board would consist of clusters as previously described. Unfortunately, that doesn't happen. Fortunately, these easy-to-count clusters are relatively simple to form by mentally moving the checkers where you want them.
One Way Mental Shifting involves moving the checkers forward to Key Points or Reference Positions and then adding the forward movement to the value of the Key Points or Reference Positions.
| Position 12: ONE WAY MENTAL SHIFTING. | |
|---|---|
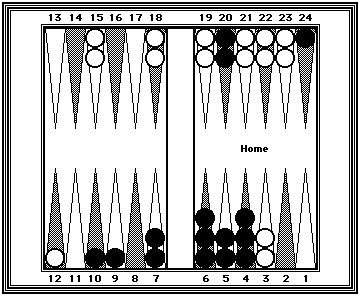 |
Black = 137 White = 121 Black's pip count of 137 can be easily counted in three clusters: 40 (eight 5s) + 33 (RP#4 + 3 pips) + 64 (three 20s + 4.) Divide White's checkers into three clusters to yield a total pip count of 121. 44 (5-Prime + 4 pips forward, 2 each from the 7-point to the 5-point) + 33 (three 10s + 3 pips from 13 to 10) + 44 (two 20s +4.) |
Note that two of White's checkers were shifted to White's 5-point which is occupied by Black's checkers. When shifting one player's checkers, the other player's checker position can be ignored.
Two Way Mental Shifting differs from One Way Mental Shifting in that checkers are shifted either forward or backward to Key Points or Reference Positions and then compensating shifts are made in the opposite direction on the same side of the board or in the same direction on the opposite side of the board. Examine Position 13:
| Position 13: TWO WAY MENTAL SHIFTING. | |
|---|---|
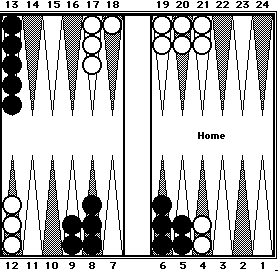 |
Black = 135. White = 142. Black's spare checkers on the 6- and 8- points are on the same side of the board. By shifting them one pip in opposite directions to the 7-point, a 5-Prime is formed. Black's position can easily be counted in two clusters: 70 (5-Prime) + 65 (five 13s) = 135. White's spare checkers on the 8- and 13-points are on opposite sides of the board. By shifting them in the same direction, in this case left to right, a 5-Prime is formed (RP#1) and RP #7 is also formed. White's position can then be counted in three clusters: 60 + 40 + 42 (two 20s + 2) = 142. |
It should be noted that there are often several Cluster Counting choices available. For instance, in Position 13, instead of forming a 5-Prime, you could have shifted the two 9-point checkers to the 8-point and compensated by shifting the two 5-point checkers to the 6-point to form RP#3. This cluster is also 70 pips.
Let's try counting some positions. Original positions and adjusted positions (after shifting) are shown but not described. Can you spot the shifts? If not, set them up on your backgammon board and they will become clear.
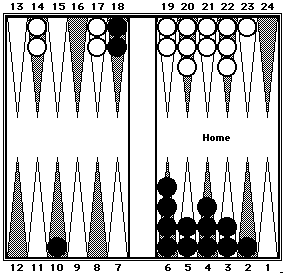
| Position 14. Black = ? White = ? |
Position 14a. By Using Two Way Mental Shifting the position becomes: |
|---|---|
 |
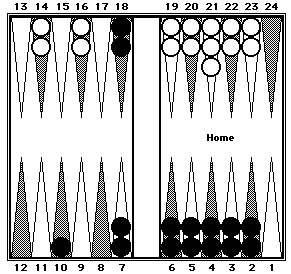 |
| Black's 100 pips can be counted in three clusters: 40 (5-Prime from the 6-point to the 2-point) + 50 (Mirrors on the 7-point and the 18-point) + 10. White's 84 pips can be counted in two clusters: 44 (5-Prime + 4) + 40 (four 10s). | |
|
| |
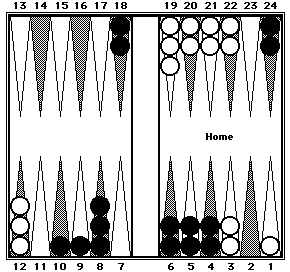
| Position 15. Black = ? |
Position 15a. After shifting, Black's position becomes: |
|---|---|
 |
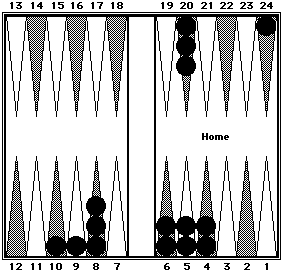 |
| Black's position can be counted in three clusters: 30 (six 5s) + 43 (RP#5 - five 8s + 3) + 84 (four 20s + 4). | |
|
| |
| Position 15. White =? |
Position 15b. After shifting, White's position becomes: |
|---|---|
 |
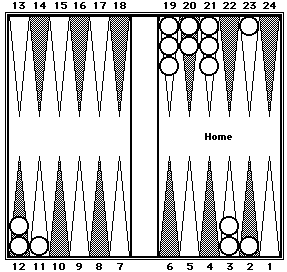 |
| White's pips can be counted in three clusters: 42 (eight 5s + 2) + 40 (RP#7) + 67 (three 20s +7). | |
|
| |
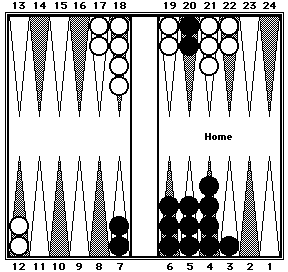
| Position 16. Black = ? White = ? |
Position 16a. After shifting, the position becomes: |
|---|---|
 |
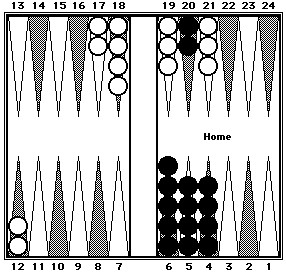 |
| Black's pips can be counted in two clusters: 66 (twelve 5s +
6) + 40 (two 20s). White's 100 pips can be counted in two clusters: 30 (six 5s) + 70 (RP#4 again + 10 for two checkers moved from the 13-point to the 8-point). Note that in Position 16a White has only 14 checkers. The two checkers originally on the 3-point were shifted in different directions - one checker to the 6-point and the other checker off the board. | |
|
| |
As previously noted, with Cluster Counting, there is almost always more than one correct way to count a position. You should use whichever cluster formations you can quickly visualize. For example:
| Position 17. Black = ? | |
|---|---|
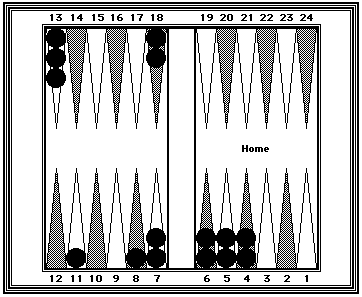 |
With a minimum of shifting, Black's pip count can be quickly counted
in several different ways: a. 63 (5-Prime +3) + 75 (five 13s + 10 by shifting two checkers from the 18-point to the 13-point); b.63 (5-Prime + 3) + 62 (RP#6) + 13 (spare checker on the 13-point); c.50 (Mirrors on the 12- and 13-points) + 50 (Mirrors on the 7- and 18-points) + 30 (six 5s) + 8 (Checker on the 8-point). |
|
| |
Well, that's the system. Certainly my list of seven Reference Positions is by no means inclusive. You probably already know or will discover other positions that can be added to the list.
Will mastering the Cluster Counting technique improve your game, or at least make one tedious aspect of backgammon more enjoyable? Count on it.
| Thanks to Jack and to Bill Davis of the Chicago Point. Thanks also to Kevin Bastian for creating the graphics for this page. And thanks to Kate McCollough for creating the HTML version of the article and putting it up on the Web. |