110 55

White 5 13 point match Blue 10

Things look pretty bleak for White. He trails by 55 pips in the race. He can lose a gammon but can't win one. At best, perhaps he will get a shot while his opponent is clearing the 4, 5, and 6-points, but then he still has to hit it. If the hit comes too late, Blue might have quite a few checkers off, or White's board might be crunched. In the actual game, both players made a huge mistake. We'll come back to this later.

Match Equity

The goal of backgammon match play is not to win each game—it is to win the match. This can be done one point at a time, or two, or four, or in whatever combination. (In actual play, backgammons are relatively rare and usually not considered in most theoretical calculations.)

We will make a few simplifying assumptions in the material that follows:

1. When the doubling cube is not in play, 20% of all games end in gammons.
   
2. The opponents in a match are of equal skill.
   
3. We will ignore the effect of backgammons and of the "free drop."
   
4. After the Crawford game, the trailer always turns the cube at his first opportunity.
   
5. If a player takes a cube in a situation where he will lose the match if he loses the game, he always immediately redoubles if he needs the extra points.

Suppose you lead 2-0 Crawford in a match to 3. Your opponent needs to win two games in a row to win the match. A gammon in the first game does not help, since he will turn the cube immediately in the next game. His chances of winning the match are therefore 50% (his chances of winning the current game) times 50% (his chances of winning the next game), or 25%. His match equity is 25%, and yours is 75%.

Now, suppose you lead 2-1 Crawford. Your opponent has another way to win—a gammon in the current game. His match equity at this point is:

10% (gammon); plus
40% (non-gammon win) times 50% (win in the next game)
or 30%, and yours is 70%.

One of the tools of top tournament players is having memorized a match equity table for matches of meaningful lengths. For the moment, readers should not worry about memorizing a table. However, a very useful match equity table appears here. The table is based on empircal results from actual tournament matches.

Match Equity Table and Drop Points (Gammonless)

We will deal with the decision to take or drop first, because it is the easier one to express mathematically.

Suppose the score is 0-0 to 3. You are doubled. Should you take?

If you drop, your match equity will be 40%. If you take, you will either be 75%, or 25%, to win. You want to take when your average equity will be greater than 40%.

For those who are inclined to algebra, we can calculate based on your winning chances (w) as:

.75w + .25 (1-w) >= .4

But a more practical way to calculate is this:

"If I take and win, I will have gained 35% match equity over dropping. If I take and lose, I will have lost 15%. Therefore I need odds of 15% divided by (15% + 35%), or 30%, to take."

For take decisions, this is the basic formula—possibly the single most important formula in backgammon:

Takepoint = Loss from taking / (Loss from taking + Gain from taking)

Match Equity Table and Drop Points (Gammon Adjusted)

Of course, gammons do matter. The actual drop point would be where your equity is less than:

100% times probability you win a gammon; plus
75% times probability you win a single game; plus
25% times probability you lose a single game; plus
0% times probability you lose a gammon.

In money play, (or in the early stages of a long match), there is an easy way to adjust for gammons, which is simply to reduce your expected winning chances by half the difference in expected gammons. (This assumes you will lose more gammons than you win, which is the usual case when you're the one being doubled.) Why half? Because when you convert a win into a gammon, you gain one point; when you convert a win into a loss, you lose two points—the one you actually lose and the one you would have won.

Gammon adjustments in match play are more complicated. We will save a discussion of gammons for a later article. For the moment—just remember to consider gammons in your taking decisions, and if you make the adjustment of subtracting 1% from your winning chances for each 2% by which you estimate your opponent will win more gammons than you do, you won't be far off.

Match Equity Table and Minimum Doubling Points

The calculation of the minimum doubling point in a match is slighly more complicated, but not overly so. And the results will probably surprise some readers.

Go back to our example of a match at the score of 0-0 to 3. If you win the game undoubled, you will be 60% likely to win the match; if you double and win you will be 75%. If you lose the game undoubled, you will be 40% likely to win, losing two points will put you at 25%. Thus, your gain when you double and win is 15%; your loss when you double and lose is 15%. The minimum doubling point is therefore:

Min. Doubling Point = Loss from doubling / (Loss from doubling + Gain from doubling)

In this case, the minimum doubling point is 50%.

When the match score is tied, the minimum doubling point will always be 50%. Let's give an example of another score, where the results are not symmetrical. Assume you are trailing 2-0 in a match to 5. Looking at the match equity table we see the following equities:

Trailing 0-3 25%
Trailing 0-4 15%
Trailing 1-2 41%
Tied 2-2 50%

Thus, when you double and win, you go from 41% match equity to 50%, a gain of 9%. When you double and lose, you go from 25% to 15%, a loss of 10%. Your minimum doubling point is therefore 10% / (10% + 9%), or 52.6%.

Value of the Cube and Market Losers

As we've seen in earlier articles, you don't necessarily double just because you have an advantage. You need to meet two other conditions. First, your gain from doubling should be larger than your loss from giving up control of the cube. Second, you should have some danger of losing your market; if your opponent will always, or almost always, take next roll, you have no need to double before this roll.

Putting It All Together—To Double Or Not To Double

So how do you really make a doubling decision in a match? Let's say you are trailing 2-0, in a match to 5.

Step 1: Are you above your minimum doubling point? As we calculated above, that is 52.6% winning chances, adjusted for gammons.

Step 2: When do you lose your market? You need to know your opponent's drop point. In this case:

• If he drops, he is leading 2-1, 59% match equity
  
• If he takes and wins he is leading 4-0, 85% match equity
  
• If he takes and loses the match is tied, 50% match equity

So his take point is Potential Loss / (Potential Loss + Potential Gain), which is 9% / (9% + 26%), or 25.7%

Therefore your doubling window is 52.6% to 74.3%.

Now, ask two more questions:

1. Can I lose my market? Usually, you need to be fairly close to the opponent's drop point in winning chances, but not always. Consider this position:

   67 72

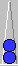
   White 2 5 point match Blue 0

   You have 14 rolls that hit and make you about 95% to win the game—so you will win about 13 times out of these 14. When you miss, you are in a virtually even race, so when you get one of the remaining 22 rolls, you will win about 11 times. You can quickly estimate your winning chances at about 24/36, or 67%. Even though you are fairly well below the opponent's drop point, you should double because a lot of the time you will lose your market next roll, and by a lot.

2. Is it worth giving up control of the cube? As discussed in earlier articles, this is a difficult concept to quantify. But you should not give up control of the cube unless you are getting a reasonably strong increase in your equity in return, by doubling in a strong position.

Putting It All Together—To Take Or Not To Take

In general, take decisions are easier. Simply, you take if your estimate of your gammon-adjusted winning chances, owning the cube, are greater than your take point. In doing this, you can use the adjustment that owning the cube generally increases your winning chances by 10%. Thus, if your takepoint is 30%, you can take with about a 27.5% winning chance since owning the cube pushes you up to about 30%.

Keep in mind though that owning a dead cube is valueless. If you are leading 1-0 in a match to 3, you cannot double out your opponent anymore. Returning the cube on 4 is pointless—your opponent cannot drop. Therefore, in this situation, where your takepoint is (you can calculate this yourself) 28.6%, you need 28.6% winning chances—not the 26% that would be the case if you could effectively return the cube.

The same consideration applies to a lesser extent at lopsided match scores. Suppose you are leading 6-2 in a match to 11, and your opponent redoubles to 4. Let's work this one out:

• Leading 6-4: Match equity 63%
  
• Tied 6-6: Match equity 50%
  
• Leading 10-2: Match equity 95%

Thus, you need 13% / (13% + 32%) or 28.9% to take. But once you own the cube on 4, your redoubles to 8 are not very powerful. If your opponent takes, he would of course immediately turn the cube to 16 (since he has nothing to lose). Since if he drops a cube his equity will be only 5%, he can take and put the match on the line with only 5% winning chances, so you lose your market only at 95% win chances. Your cube ownership thus becomes considerably less powerful in this case, and you should not give it much weight in the decision to take.

Another Example

The example we gave for the score 2-0 to 5 gave us a doubling window close to a money game (50% to 75%). Let's look at a different example.

Suppose you are trailing 3-1 to 5. Going back to the match equity table we find:

• Trailing 4-1: Match equity 17%
  
• Trailing 5-1: Match equity 0%
  
• Trailing 3-2: Match equity 40%
  
• Tied 3-3: Match equity 50%

In this case, your gain is 10% and your loss is 17%, so you need 17% / 27%, or 63% to double. Your opponent's drop point is calculated as 10% / 50%, or 20%. So your doubling window opens at 63% winning chances and you lose your market at 80%.

Match Equity Calculation

There is one final, minor point, to address. Match equity is solely a function of the number of points remaining in the match. A score of 38-37 in a match to 41 is the same as a score of 2-1 in a match to 5. Match equities are typically thought of in terms of "away" numbers—a score of 2-1 to 5 is "3-away/4-away."

Wrapping It Up

Does all this matter? Yes, Yes, a thousand times Yes.

There is probably no single greater difference between good tournament players and world-class ones than their mastery of match equity tables and ability to use them over the board. If you can squeeze out a few percent of extra match equity here and a few percent there by correct doubles or takes, you will win that many more matches. Consider the score we talked about above, leading 1-0 to 3. If you are doubled and take with the 22.5% winning chances that you "know" are right without considering the state of the match, your match-winning chances will be:

22.5% * 100% + 77.5% * 30% = 45.75%

Knowing to correctly drop in this situation means winning 4% more matches than you will otherwise. Over time, that adds up to a lot of matches.

Quiz Answer

Let's go back to the earlier problem. In a money game, Blue is too good to double. He has some gammon chances, and he has no sequence of rolls that could result in his opponent being able to take next turn. He might well double in the near future, but for now he should play on for a gammon. A double would not be a huge error, but it would be a clear one.

In the actual game, Blue doubled. Let's think about this doubling decision for a moment:

First, should White take?

• Drop: Trails 8-away/1-away, match equity 6%
  
• Take (and no-cost redouble) and lose: Match equity 0%
  
• Take (and no-cost redouble) and win: Match equity 100%

Clearly, White needs only 6% winning chances in this game to take the cube. Surely he has that. Now, should Blue double?

• No double and win: Leads 8-away/1-away, match equity 94%
  
• No double and lose: Leads 6-away/3-away, match equity 71%
  
• Double and win: Match equity 100%
  
• Double and lose: Match equity 0%
  

By loss / (loss + gain), Blue needs 71% / (71% + 6%), or 92.2% to double. I rather doubt his chances are that good. (Jellyfish makes Blue's winning chances 87.4%). Further, sometimes Blue will win a gammon (10.9% according to Jellyfish), in which case his gain from doubling is even smaller, making his doubling window even narrower.

So, if Blue holds the cube, and Jellyfish is right, Blue's match-winning chances are:

10.9% gammon wins, plus
76.5% simple wins times 94%, plus
12.6% simple losses times 71%

for a total of 91.8%. By doubling, he gave his opponent a chance to take and play for the match, lowering his match-winning chances to 87.4%. His double lost 4.4% in match-winning chances. On the other hand, White's incorrect drop cost him even more—6.6% match-winning chances.

So a fairly simple money decision—too good to double / pass—becomes an entirely different result when put in the context of the match score. The position is now not good enough to double, and is a clear take and redouble.

In our next article we will discuss some more concepts of match doubling theory, including gammon prices, free drops, and special match scores. We will also present a table of doubling windows for matches up to 5 points.
 

Next Article: Doubling Windows and Special Doubling Situations.

Practical Backgammon is a column for beginning and intermediate players. Its goal is to offer specific solutions to common backgammon situations, and to provide the tools for advancing players to make use of more advanced material.