Erhvervsvejlederen

At være lejemorder er slet ikke som de fleste tror. Mange forestiller sig f.eks. at våbenet spiller en helt central rolle. Det er vigtigt, selvfølgelig, men på en anden måde end de fleste regner med. På film ser man ofte hvordan lejemorderen opvarer sit præcisionsvåben i en specialfremstillet attachetaske. Den ligner lidt de kufferter topnøglesæt leveres i. Med hver del anbragt sirligt i sin egen lille fordybning så al ting ligger pænt og ordentligt. Filmlejemorderen åbner højtideligt sin taske og samler omhyggligt sit våben. Jeg er sikker på, du har set den klassiske scene hvor skydevåbenet med rutinerede bevægelser samles stykke for stykke. Til sidst monteres kikkertsigtet, der gør mesterskytten i stand til at ramme en gråspurv i røven på flere hundrede meters afstand. Det hele er sat sammen så der langsomt bygges et klimaks op omkring det øjeblik hvor skytten får sit bytte i sigte og forsigtigt krummer fingeren om aftrækkeren. Det spændende er selvfølgelig om offeret i det afgørende øjeblik bukker sig ned eller forsvinder fra synsvinklen.

Jeg håber ikke, jeg skuffer dig, når jeg fortæller at sådan er det slet ikke i virkeligheden. En lejemorder bruger som regel kun sit våben én gang. Alene af den grund er der selvfølgelig ikke tale om et stykke raffineret præcisionsteknologi, men typisk om et relativt billigt, serieproduceret standardskydevåben. Og offeret nedlægges som regel på klods hold; ikke noget med 200 meters mesterskud. Hvis der altså i det hele taget benyttes skydevåben, hvilket nok hører til undtagelserne.

Personligt undgår jeg helst skydevåben. De er besværlige at anskaffe uden at sælgeren vil udgøre en potentiel sikkerhedsrisiko, de skal skaffes af vejen efter jobbet så de med garanti aldrig findes igen, og de fremprovokerer typisk en ret stor efterforskning fra myndighedernes side. Enkle metoder er efter min bedste faglige vurdering langt bedre. Man kommer langt med et blyrør eller en spejderkniv. Det stiller krav om tæt kontakt med subjektet, men det er som regel intet problem. Skydevåben bruges mest efter kundes ønske, eller hvis det kan være umuligt eller for risikabelt at komme rigtig tæt på. Brug af skydevåben koster altid ekstra.

Er du som folk er flest, vil du sikkert gerne kende prisen. Du vil vide hvad det koster at løse et problem af den slags der går på to ben. Det er ingen hemmelighed. Grundtaksten er 80.000. For 80 små stykker papir med den rette dekoration vil jeg slutte en skæbne for dig. Særlige krav til metoden, tidspunktet, oprydningsarbejdet, spor, rejser, etc. koster ekstra. Der kan også blive tale om risikotillæg hvis subjektet er en berømthed. Alt i alt løber det hurtigt op, men du ville blive forbavset over, hvor løst pengene sider. Hvis bare problemet er stort nok. Den største opgave jeg har haft var på 900.000 og strakte sig over det meste af seks uger. Når jeg tænker tilbage, var prisen nok for lav, omstæmdighederne taget i betragtning. Seks små, lette jobs à 150.000 er klart at foretrække. Som nu f.eks. det jeg sidder og venter på at fuldføre, mens jeg i tankerne fortæller dig disse ting.

Staying Ahead

Taking doubles when leading
in long backgammon matches

by Lasse H. Madsen

This text deals with a common problem in tournament backgammon: How to protect a lead in a long match, e.g. when the match might still have a long way to go. For now, the main focus is on taking doubles when leading in the match. First we’ll have a look at accepting initial doubles when leading in the match; then we turn to accepting redoubles.

The approach I’m going to take is a general one. I won’t be explaining how to calculate take points, and I won’t be presenting lots of numbers, formulas and algebra. Plenty of excellent sources for that sort of thing are already available, many right here on GammOnLine. Rather, I’ll be presenting charts showing the patterns of how the match score influences take points, and develop some general guidelines, along with some practical examples.

The reason for this approach is that I’m having a really hard time doing match equity calculations over the board under tournament conditions. Back home at my desk, with pen, paper and spreadsheet¾heysure, no problem. At the quarterfinals in the average regional tournament, after eight hours of play, with a crowd of kibitzers watching and mumbling, possibly under time pressure, it’s a different story. If you feel the same way at all, please read on. Since the approach I take is kind of an experiment, I’d be more that happy to receive some feedback as to whether or not it’s a useful way to present the information.

Accepting initial doubles with a match lead

Generally speaking, a match lead should not make too big a difference in your taking policy when we’re taking initial doubles. What might make a small difference is that gammons usually are more costly than normal, and that you don’t get as efficient redoubles as usually. How big are those factors?

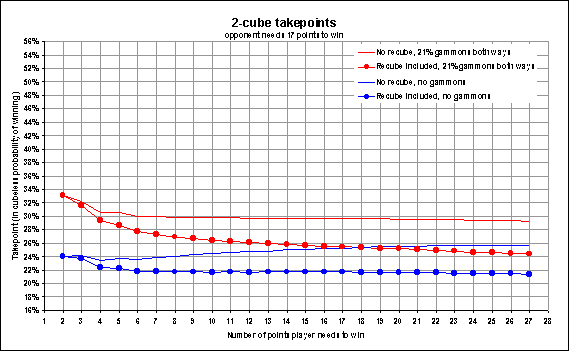
The chart shows the winning chances you need to accept a 2-cube when your opponents still has 17 point to go. The blue curves indicate no-gammon situations; the red ones assume that 21% of either players wins will be gammons. Of course this is seldom going to be exactly the case, but it gives an idea of the effect of gammon, in many opening and middle game situations. The lines with markers indicate the cube equity is taken into account, thus producing a lower take point (measured in cubeless probability of winning, CPW¾sometimes also referred to as cubeless game winning chances, cgwc).

We’re looking at the big picture here, so the chart includes all scores right from 2-away, 17-away to 27-away, 17-away. (The opponent score is held constant at 17-away, while the player, whose take strategy we’re examining, is treated as a variable).

In the simple case, where there are no gammons and no recube equity, as in, say, a last roll bear off situations, the chart indicates that you will generally need around 25% to accept a cube, just as in money game. No big surprise here. It should be noted, however, that as the match lead increases it becomes slightly more attractive to accept an initial double under these conditions. It’s not a big deal, however, but at 6-away, 17-away, the leader should be able to accept an initial double in a last roll bear off situation with about 24% winning chances rather than the usual 25%. Few people will be able to judge winning chances that accurately, so in practice this is not too important.

When we grant the leader cube access it becomes a bit easier to accept the initial double; the take point is just shy of 22% cubeless winning chances, just as in money game. (See the blue curve with markers). The value of owning the cube diminishes, however, as the end of the match approaches, since the leader would be reluctant to redouble to four: Notice how the distance between the blue lines gets smaller as the lead gets bigger. Obviously, when the leader needs only two points to win, he gets no cube value at all. The main point to notice is that the take points are still pretty much as in money game, with a small exception when the leader can’t take advantage of cube ownership.

When gammons are included (at the rate of 21% for both sides) we still have pretty much a money game situation, except when very close to the end of the match. The worst situation for the leader is at 2-away, 17-away where the lead is really big and where he gets no recube equity at all. In this case he needs about 33% winning chances to justify a take, and that’s quite different from the roughly 26% he’d need at money game or further away from the end of the match, where he could put the cube to some use.

Before we turn to some actual examples, let’s try to summarize what we’ve learned so far about accepting initial double with a match lead:

· It’s not the size of the lead but the number of points still needed to go that has the greatest effect on the leader’s take point.

· With lots of point to go, even a big lead shouldn’t cause the leader to be more cautious in accepting doubles when gammons are unlikely.

· With lots of points to go, a big lead should cause the leader to be only slightly more cautious, in accepting gammonish doubles; the takepoint is typically about 2 percentage points higher compared to even scores.

· Near the end of the match, when the leader is within about five point of victory, his take points increases a little (1-2 percentage points) for non-gammonish positions, and a good deal (2-5 percentage points) for gammonish positions.

· With a big lead you can take a last roll bear off position with slightly less than 25% winning chances.

Let’s take a look at a couple of examples of this:

The first position is taken from Kit Woolsey’s article Reference Positions, from GammOnLine. Being 20 pips down, and the other guy with lots of time, White has only a small take for money, says Woolsey. Since gammons are extremely unlikely in this position, we now know that White should have a take also at virtually any match score, with the possible exception of being 2 or 3 points within victory, since the take might depend on being able to redouble, should the game turn around. That is indeed an accurate assessment; White should take with any kind of lead in the match, except when he’s 2-away or 3-away; in that case he has small pass.

When gammons are a real possibility, things are not quite as happy for the leader, even at initial doubles:

For money, White should have a reasonable take here, although not a particularly happy one. It’s easy to see people passing this one. Gammons are very possible, but with the anchor and not too many blots around for Orange to scoop up, it’s not as if White is grave gammon danger. So White takes in a money game and at any even match score with lots of points to go. With a big lead, however, White might have a pass, based on the gammon risk. If you think the take is really borderline in the first place, then a pretty small lead like, say, 12-away, 17-away could turn it into a pass. It you think the take is pretty clear, you would either need a really big lead, like 6-away, 17-away to justify a pass, or to be close to the end of the match, like 4-away, 8-away. At the double-edged 2- and 3-away scores, you would most likely not want to take this one.

The point here is not so much exactly what White’s winning chances are, and what the precise take point at all conceivable scores would be. We’re trying to build a general feel for just how much more cautious the leader should be.

I wouldn’t claim to know the theoretical correct cube play at various scores, but an educated guess would be that White can take the double unless he’s within six points of victory and leading substantially. With an extremely large lead, in, say, a 27-point match, he might have a pass a bit before that.

Suppose we weaken Orange’s position, by giving him four checkers on the 20-point, while doing damage to his racing lead:

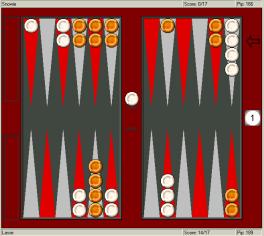
In this position White should have a pretty clear take for money and at almost any match score, with the exception of the notorious 2- or 3-points away. When White is 2- or 3-away and enjoying only a small lead, like [2-away, 4-away]; [2-away, 5-away]; [3-away, 5-away] or something like that, he has a rather big pass, since Orange is now threatening to win the match or take the lead by winning a gammon, which is still not too unlikely. 2-away, 10-away, for instance, would probably also be a pass, but not nearly as big as at 2-away 4-away where Orange’s gammons operate at maximum efficiency.

Next is a simple position illustrating one of the finer points of taking with a match lead:

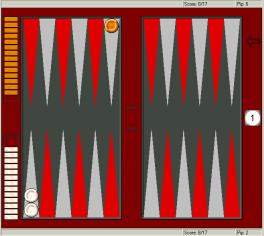
As most players are aware, for money this last roll situation is a true borderline take/pass decision. What fewer know, however, is that it doesn’t take much of a match lead to turn it into a take. With a 5-point lead or more, White has a pretty clear, although still small, take. Don’t overestimate this effect, though. Pure 3-roll positions are still passes, with any kind of lead, for example. (In fact, initial doubles in 3-roll positions can’t be taken at any match score, unless there’s an automatic redouble available). Also, note that this really only works in last roll positions; in longer bearoffs the diminishing cube leverage for the leader would balance the slight incentive to take more aggressively.

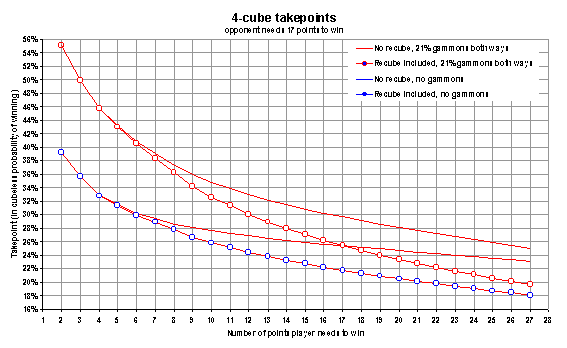
Now it’s time take a closer look at the scores where the leader is near the end of the match. In the next chart, we’ll fix the leaders score at two, three, four, and five points away while treating the opponents score as a variable. This may be a bit confusing at first, since the x-axis is now the other guy’s score, rather than ours, so take your time to familiarize yourself with the chart.

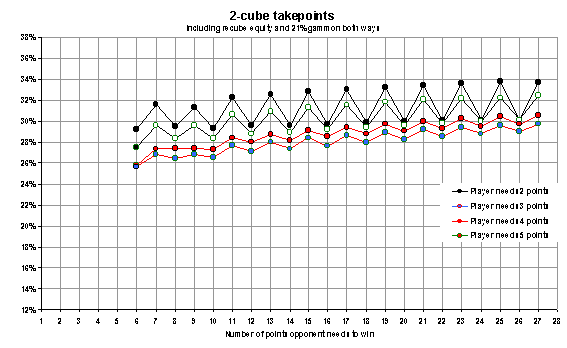
From chart 1 we know that when you need four or five points to win, your takepoint is somewhat higher when you enjoy a big lead and face a gammonish initial double. Chart 2 verifies our suspicion that the bigger the lead, the more true this is. The red and green curves clearly indicate higher take point when the opponent needs lots of points to win. It’s not a dramatic effect, though; each extra point you’re leading raises you takepoint by only about one sixth of a percentage point. For example a 6 point lead, 4-away, 10-away suggest a take point of about 27%, compared to the roughly 26% you’d need at 4-away 4-away (taking into account gammons and recube potential).

What’s really interesting about chart 2, though, is the cyclic pattern the curves depict, especially at when the leader is two points from victory. This suggests that it’s actually easier to accept an initial double, even a moderately gammonish one, when the opponent has an even number of points to go. That’s quite counter intuitive, since after the Crawford-game the leader has a free pass whenever the opponent has an even number of points left. But when you’re two points away it’s almost the other way around: You’d rather take when the trailer needs an even number than if he’s an odd number away. At 2-away, even-away the take point is generally about 2 percentage points lower, than at 2-away odd-away. With a really big lead the difference between even-away and odd-away is as big as 4 percentage points.

Let’s se a couple of examples of this phenomenon:

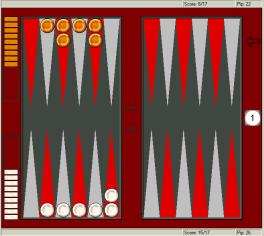
In the above diagram, White is trailing by four pips, 26 to 22, which is pretty serious in a race this short. For money, and at most match scores, White would probably have a small pass, winning 21.1% cubeless according to one database. Being 2-away with a big lead changes things, however. White should pass if Orange needs 7, 9, 11, 13, 15, 17, 19 or 21 points to win, but take if Orange needs 8, 10, 12, 14, 16, 18, 20 or 22 points. That’s kind of funny, but it seems to hold up to further analysis.

It should be noted, however, that this principlephenomenon only occurs when White is holding a sizeable lead. If Orange needs 4, 5 or 6 point to go, White has a pretty low takepoint, around 20%, as long as gammons are not possible. If Orange on the other hand needs 2 or 3 point, White would be quick to pass, with takepoints of 30% and 28% respectively.

The same pattern can, perhaps surprisingly, be seen in positions with some gammons chances:

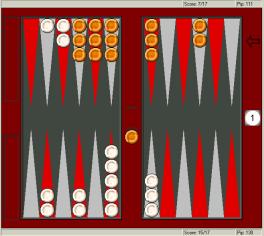
In the above position White is a distinctbig underdog, it’s pretty volatile, so for money and in most match situations Orange has a fine double. White, on the other hand, has several ways to win, is not in particular gammon danger and should have a reasonable clear take. If White leads and need only 2 point to win and hence can’t win a gammon or redouble after taking, it might be another story. Chart 2 suggest that White will usually need at least 30% winning chances in order to take a moderately gammonish initial double when leading 2-away, something-away. That’s considerable more than he’ll need at an even score, and it’s hard to say if it’s there. As it turns out, While probably has a small take if Orange needs an even number of points, and at least 6, while he should pass if Orange needs an odd number greater than or equal to 7.

With a smaller lead, when White needs 3, 4 or 5 points, White is better off passing.

The concept of adjusting one’s taking policy to whether the opponent needs an odd or an even number of points applies when the leader needs 2 or 3 points. It’s a delicate thing, however, and should be applied very carefully, i.e. when breaking ties in otherwise close decisions.

Accepting redoubles with a match lead

As we might expect the take point for redoubles are more strongly influenced by match score than initial doubles. Let’s again fix the trailers score at 17-away, and see what happens when the leader a) expands his lead; b) gets closer to the end of the match.

First of all, the size of the lead now has a profound effect on the leaders take point, especially if a gammon is possible. In that case the leaders take point increases by about 1 percentage point for every point he’s leading. And when we get closer to the end of the match, it’s more like 2 percentage points for every match point lead. Real close to the end of the match things are pretty extreme; if you ever happen to double your opponent at 2-away 17-away in an gammonish position you’d better pray for a good roll well, for you’ll need to be a clear favorite to accept his automatic recube next turn. (Of course this example is a bit academic, since most people would be sophisticated enough not to double in the first place).

Second, note that in the case of a non-gammonish position, the same pattern holds, although to a lesser degree. A one point lead still corresponds roughly to an increase in take point by about 1 percentage points, but we need to get pretty close to the end of the match to see take points much higher than 30%. Notice that the leader’s recube equity is not totally insignificant until the leader is close to handling the trainer and automatic redouble to the 16-level. For example, at 12-away, 17-away the trailer will still need about 14% to accept an 8-cube, and that’s enough to give the leader some recube equity so he’ll take with about 24% rather than the 27% he’d need in a last roll position.

A summary of taking redouble before we turn to examples:

· With a match lead, even a small one, be slightly cautious of accepting redoubles in gammon free positions, and very cautious in gammonish positions.

· As a rule of thumb, your take point increases with about one percentage point for each point you lead, when there’s still a long way to go.

· Typically it takes around 30% or more to accept a gammonish redouble when leading. And make that 40% when you’re leading substantially and within 6 points of victory.

· In non-gammonish positions, take almost like in money game until within 6 points; after that you need to be careful, with a take point of at 30-40%

· If you’re within 8 points of victory don’t figure in any recube equity (redoubling would mean playing for 16-point and most likely the match).

Let’s see some actual positions:

This position is an almost perfect 5-roll bearoff (double aces don’t necessarily work); White wins with probability 28.1% and has a clear take for money of course. What kind of match lead might cause some doubt on the take? Since the take is so clear to begin with, we need a pretty big lead to change that. Note that with a big match lead White gets no value from the cube, he might not even be able to redouble (to 8) in a 2-roll position. So basically the question is: By how much should White be leading to raise his take point from below 25% to 28% cubeless? One possible answer would be a 10 point lead, 7-away 17-away, as can be seen from chart 2. With an even bigger lead he would have a clear pass. As always, when we get closer to the end of the match, the take gets harder. For instance White would pass at 5-away 11-away also, even though his lead is smaller than 10 points.

When gammons are an issue, a smaller lead might make the difference:

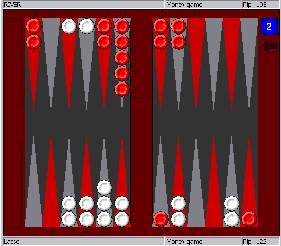
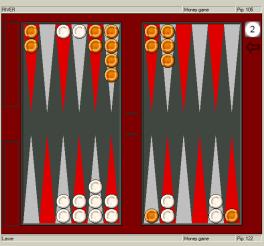
Here, OrangeRed has a nice redouble based on a combination of a racing lead and some attacking chances. White will normally have an OK take, since there are some immediate strong shots if OrangeRed fails to clear up his blots. With a match lead, however, the combination of a four-cube and a gammon threat could make it a pass. With only a two- or three-point lead, 10-away, 12-away, for instance, the take is quite borderline. With a bigger lead or closer to the end of the match, White will usually have a pass. 10-away, 17-away would be a clear pass, and so would 6-away, 8-away. If White is both close to winning and enjoys a big lead, like 6-away, 17-away, taking becomes a huge blunder.

Let’s do one more:

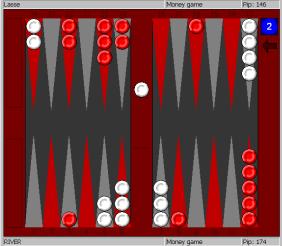
This time, for money White has a bigger take than before, in fact, the redouble may technically be quite close, although it’s certainly a good practical double. Red is a bit short of ammo so his game is not quite as strong as it looks. With a match lead, however, this is somewhat balanced by the fact that OrangeRed has a significant gammon threat; maybe about one third of his wins will be gammons. As a consequence White’s proper strategy is quite similar to the previous position: With a lead of two or three points he should consider passing even in a match with long way to go. With a bigger lead or when approaching the final stages, say at 6-away, passing becomes mandatory.

Methodological note

The match equity table. All numbers and charts presented here are based on a match equity table I computed some years ago. The reason I’m not using Woolsey’s table is that it doesn’t go further than 15 point and that it doesn’t have decimals. The problem is that even though everybody agrees that match equity tables are not accurate to one decimal point, this is the accuracy you need to calculate meaningful take points at certain scores. Take points at loop sided scores depend critically on the exact numbers in the match equity table used, since small differences and rounding errors are magnified in the calculations.

To see this, suppose for instance that we want to calculate take point at 2-away, 13-away. We might use numbers from Kit Woolsey’s table with no decimals, or we could use my computer generated table with one decimal point:

Woolsey Madsen

Leader passes for 2-away, 12-away 95% 95,4%

Leader takes and wins for victory 100% 100,0%

Leader takes and loses for 2-away 11-away 94% 94,0%

Gain from taking and winning 5% 4,6%

Loss from taking and losing 1% 1,4%

Take point 17% 23,3%

That’s quite a difference. When the gains and losses are small, it doesn’t take much of an error to impact the loss:gain ratio dramatically. For this reason you won’t be able to use Woolsey’s table to confirm the point about the 2-away even-away score, where the leader should take more aggressively than at 2-away, odd-away¾we simply need greater accuracy at these scores.

My table was generated using an iterative algorithm, starting off with a cubeless match equity table, then repeatedly adjusting it to reflect asymmetric cube leverage until a stable table emerged. I can’t be sure, of course, that it’s any better than the next guy’s, but it does seem to produce quite consistent results. I’d be happy to mail a copy to anybody interested.

Cube leverage. I use a simple, recursive formula to estimate cube leverage for any give match score and cube level. It takes into account whatever level the cube might meaningfully get to, and assumes 60% cube efficiency on average. Again, it’s not completely clear that the underlying model is accurate or if there might be some better approach, but to me the results look reasonable, and besides I couldn’t come up with anything than works better. The key is, I think, that it gives a good feel for the dynamic of taking strategy in various situations¾even though the take points (that are average figures anyway) might be shown to be off by a little.

Rollouts. I used computer rollouts to verify the conclusions in the text, so they shouldn’t be too far off. However, the exact difference between cube action at various match scores depends somewhat on the match equity table used, and on the method used to convert cubeless figures to correct cube action. It’s possible that different robots will give slightly different answers, even based on rollout results. I couldn’t do the ideal, true live cube score based rollouts, but I think the results should be reasonably accurate.