Fair Settlement
In Backgammon
Play
1.
Introduction
Occasionally,
backgammon players run into situations when a settlement is desired toward the
end of a chouette or money game. When
one or two more rolls would determine the fate of a game with a high cube
value, players prefer sometimes to settle in order to cut their loss instead of
riding a large risk.
Judges
in situations can also seek settlements when conflict arises between two
players.
Settlement
agreements can be affected by non-mathematical factors associated with the
players’ characters such as one’s superiority over the other, one’s
disposition, their current scores, and so on.
However, there is always a ground for fairly calculated settlements with
no regards to such external factors.
The
study in this paper aims to determine a mathematical formula, and consequently
a table, for settlements that seek mutual fairness to both players, which is
based only on the assets of the game being played.
2.
Theorem of Fair Settlements
Players
have accustomed to calculate their chances of hitting checkers in terms of the
number of rolls out of 36, rather than in terms of percentage values. The following theorem is established on this
ground, although the correspondence with the percentage system is simple in
many cases.
2.1. Theorem:
In a
backgammon game, let P, B and S refer to the following entities:
P: the number of chances, out of 36, for
winning the game,
Q: the current cube value of the
game.
S: the fair settlement value of the game.
If
there is no chance for a gammon, then S is determined by the following formula:
S = (1 - P/18) * Q.
2.2. Proof:
Notice, first,
that the theorem requires a no gammon chance, be it a gain or a loss. If so, the settlement value would increase
in a way based on the scale of the gammon potential. Section 7, Gammon Possibilities, discusses this point
further. From now on, no gammon is
assumed.
In theory, if
36 games identical to the game in question are played, then P games would be
won and 36-P games would be lost. The
amount of points won would be P*Q, and the amount of points lost would be
(36–P)*Q. In total, the combined win
and loss points would then be:
P*Q - (36–P)*Q
i.e. 2P*Q – 36Q
Therefore, the
average settlement value of a single game would be:
S = (2P*Q – 36Q) / 36
i.e. S = [(P-18)/18] * Q
Whether S is
positive or negative depends, of course, on the winning side. That would then indicate whether P-18 is
positive or negative, or equivalently whether P is greater or less than
18.
In order to
produce a positive settlement value, let P be less than 18. Then:
S = [(18-P)/18] * Q.
After a
simplification by 18, the equivalent formula would take its final form:
S = (1 – P/18) * Q
2.3.
Illustration:
P = 5; Q =
64. ==>
S
= [(18 - 5) / 18] * 64 = 46.22
3. Initial
Settlement Table
To produce a
settlement table, values for P and Q must be given.
3.1. P Values
P values run
from 0 to 36. The 0 and 36 values must
obviously be eliminated because of the perfect winning certainty. Also, the P values from 19 to 35 essentially
generate settlements equal to those of the opponent player from 17 to 1,
respectively. Therefore, the two series
of settlement values differ in their sign only.
As a result,
the P values worth being considered are those from 1 to 17 only.
3.2. Q Values
In order to
draw a single settlement table, only one cube value must be considered. Furthermore, an easy table must allow the
players to extract settlements for other desired cube values.
The cube value
of 16 seems to be a convenient choice.
Let’s explain why.
Q values are
powers of 2. The number 16 has a
special place among frequent cube values when settlements are desired. As the fourth power of 2, the number 16
stands in the middle of a series of cube values 4, 8, 16, 32, and 64. This particularity allows an easy extraction
of settlement values for the other four cube values. The reason is that the settlement for any desired one of these
cube values could be extracted from the table by easily dividing or
multiplying the answer by 2, once or twice. This can hopefully be done on the fly, while
playing.
So with the Q
value set to 16 and the P values running from 1 to 17, the settlement table
looks as follows:
|
4. Refined
Settlement Table
In
this section, we’ll develop a settlement table that would be easy to
remember.
The
obvious thing to start with is to round the S values to their closest integral
values. Doing that would turn
fractional numbers such as 15.11, 9.77 and 4.44, for examples, to whole numbers
15, 10 and 4, respectively.
This
approximation carries an error percentage with every whole number. The error percentage is calculated as
follows, where Sa denotes the adjusted settlement:
Absolute value of (Sa –
S) / Sa.
The
next form of the table adds to the previous one the new settlement numbers and
their corresponding error percentages:
|
By
inspecting column # 4, we notice that the errors fall in two ranges: 0.00% to
6.66%, and 11.00% to 12.00%. Whereas
the first range is quite reasonable, the second one carries some surplus with
it.
Notice
the following facts about the error column:
- The top
twelve numbers fall within the low 6.66% error. This is a very good approximation.
- Only five
values fall in the high 11%-to-12% error range.
When
an accuracy of 11%-to-12% is not close enough, players must remember that the P
values involved are those highest five, from 13 to 17.
This
should make us feel comfortable with the settlement values in the Sa
column.
Now
let’s drop from the table the columns carrying the fractional settlements and
errors, keeping only the columns with whole numbers.
The
final form of the settlement table that we have been working on now looks as
follows (For convenience, the Sa title has
been renamed S.):
|
5.
Settlement Rules
The
table is good enough as a reference, but it may not be simple enough to know by
heart. In this section, we will develop
rules that have the merit to help players memorize the settlement numbers. The rules will be drawn from a series of
observations.
Observation
#1
Notice
that while P values increase from 1 to 17, S values decrease from
15 to 1. This observation leads to the
foundation rule:
Rule #1 (Foundation Rule): The lower the chances, the higher the settlement.
Observation
#2
The
table has a central line. It’s where P
and S carry their mid-values of 9 and 8 respectively. Try to remember this line.
In
the game, the central line simply means that when your chance of winning is 9
(out of 36) then the settlement value would be exactly 8. If you recall that the table’s default cube
value is 16, then the central line translates into the second rule:
Rule #2 (Basic Rule): For a winning chance of 25%, the fair settlement is 50% of the cube value.
As
ground for the next two observations, imagine the 17 rows partitioned into
three sections: First 4, then middle 9, then last 4. We’ll call this partition the 4-9-4 partition (See the
highlighted figure below):
- Rows 1 to
4
- Rows 5 to
13
- Rows 14
to 17
|
To
remember this partition, just bear in mind the numbers 5 and 13.
Observation
#3
Notice
that S repeats the same value as it moves from one section to the next. The P values of 4 and 5 share the settlement
value of 12; also, the P values of 13 and 14 share the settlement value of
4.
In
the game, this means that having 4 or 5 good rolls to win yields the same 75%
settlement of the cube value.
Similarly, 13 or 14 good rolls yield the same 25% settlement of the cube
value.
If
we notice that 4 or 5 rolls actually translate to a 12.5% chance (one eighth),
and that 13 or 14 rolls translate to 37.5% (three eighths), then we can list
two new rules:
Rule #3: For a winning chance of 12.5%,
the fair settlement is 75%. (6 times the cube value)
Rule #4: For a winning chance of 37.5%,
the fair settlement is 25%. (Only 2/3 of the cube value)
Observation
#4
Notice,
in the 4-9-4 partition above, that S is equal to 16-P in section
a, to 17-P in section b, and to 18-P in section
c. This subtraction gives way to an
easy method to reach settlements for all P values from 1 to 17. This observation leads to rules for the most
frequent situations:
For
the reader’s convenience, the settlement table and the settlement rules are
separately collected at the end of the article.
6.
Applications
Exercise
1:
You
and your opponent are bearing off. You
have 2 checkers on point 1 and he has 3 checkers on point 2. It’s his roll and the cube is on 8, his
side. He offers to settle. What’s a fair settlement figure?
Answer 1:
The
opponent’s chance of winning is 5 out of 36 (any set but 1-1). Because 5 is in the middle section then the
settlement is 17-5= 12 (Mid-Section Rule).
Knowing that the cube value of 8 is half of the default cube value of
16, the answer would be half of 12, namely 6.
Exercise
2:
You
figure out that any roll of 2 (direct or combined) would give you a win in a
game with a cube value of 32 on your side.
You desire to settle. What would
be a fair settlement?
Answer 2:
With
twelve chances to roll 2 (any 2, or 1-1), P is equal to 12. Since 12 is in mid-section, S will be 17-12
= 5. Since the cube is at 32, a fair
settlement would be to pay 10 points.
Exercise
3:
What’s
a fair settlement for a 40% chance of winning a game with a cube on 64?
Answer 3:
On
the fly, we figure out that 40% out of 36 is somewhere between 14 and 15. Say
14.5. Remember that 14.5 is in the
upper quarter. The High-Section Rule
determines S as 18-13.5, i.e. 3.5.
Since the number 64 is 4 times the number 16 then multiply 3.5 by 2
twice. The answer is to give 14.
Recall
that the upper P quarter has an 11%-to-12% error range. This means the settlement of 14 could as
well be any number from 12 to 16.
7.
Gammon Possibilities
This
point is very important to bear in mind before using the settlement table. A settlement must take into consideration
whether a gammon could occur in case of a miss. If it does, the amount of loss increases remarkably, and therefore
the formula generated above should not be applied.
Is
it possible to generate a formula for the case of a gammon possibility?
The
answer depends on whether more information can be provided. We need to know the percentage of gammon
possibility in case of a miss. Of
course, building a formula for all possibilities is beyond our purposes, but it
is possible to consider one special case.
That case is when a 100% gammon loss would occur if a miss occurs. We must indicate that such a situation is
infrequent, but we will discuss it in order to draw a comparison with the above
discussion.
The
idea will take us back to the proof of the Fair Settlement theorem. Theoretically speaking, if 36 identical
games are played, then P games would win the face value of the cube each, and
36-P games would loose double the face value each. The theoretical total point result would then be:
P*Q –
(36-P)*Q*2
(Notice
the multiplication by 2 for the loss.)
By simplifying the expression, the total becomes:
3PQ – 72Q
When
we divide by 36, the theoretical value of a single game would then be equal to:
S = (PQ-
24Q)/12
We
notice that S becomes zero when P is 24.
So, a tie occurs when the underdog player holds 24 out of the 36 cards,
namely two thirds. (Remember that in
the case of no gammon the winning frequency was only half the games.) In the long run, the underdog gets paid only
one third of such games, namely from P = 25 to P = 36.
Like
we did in the case of no gammon, if we take P in the lower segment, i.e. less
than 24, then the formula would be:
S =
(24Q-PQ)/12
By
setting the cube value to 16, like we did in the no-gammon section, we conclude
the formula:
S = 32 – 4P/3
= 32 – 1.33 P
(Compare
this formula to the previous formula, S = 16 – 0.89 P.)
The
table for the new formula is not as attractive as that of the no-gammon
case. However, it would give a clear
idea if we draw the curves of the two formulas on the same graph. The next graph shows how the gammon and
no-gammon formulas would compare to each other.
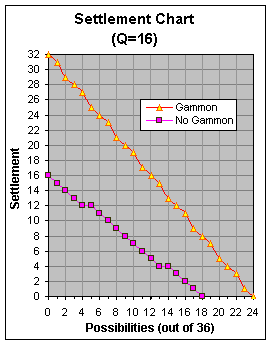
As
you can see, the settlement price gets much higher when a gammon is possible.
8.
Conclusion
The
study generates a mathematical formula to calculate fair settlements for
chouette games. The formula is based on
two input items, the cube value and the chance of winning the game. From the formula, an easy-to-remember table
was drawn, and a set of rules was derived.
The
focus of the study is on the assumption of no gammon. However, a section on the possibility of gammon is presented at
the end.
|
Rule #1 (Foundation Rule):
The lower the chances, the higher the settlement.
Rule #2 (Basic Rule):
For a winning chance of 25%, the fair settlement is 50% of the cube value.
Rule #3:
For
a winning chance of 12.5%, the fair settlement is 75%. (6 times the
cube value)
Rule #4:
For
a winning chance of 37.5%, the fair settlement is 25%. (Only 2/3 of
the cube value)