Cube Handling
In Noncontact Positions

Tom Keith,  June 2004

In this article I describe and evaluate several popular methods of making cube decisions in noncontact positions. To compare the methods, I use real positions from real games. In this way, the types of positions which occur often in actual play are weighed more heavily than positions that happen only rarely. All positions were rolled out by computer to obtain accurate cubeless and cubeful equities.

Five different pip-adjusting formulas are evaluated—the Thorp count, the Keeler/Gillogly count, the Ward count, the Lamford/Gasquoine count, and my own "Keith" count. The formulas are judged on their ability to account for wastage and on their ability to make accurate cube decisions.

Finally, I give some information on converting between cubeless and cubeful equity.

If you have comments or questions on this article, please send e-mail to tom@bkgm.com.

 

Database of Positions

The positions collected for the database come from three sources:

  • Mark Damish's Big_Brother database of games played on FIBS.
  • François Hochedé's LittleSister database of games played on FIBS.
  • Games played on FIBS by my backgammon program, Motif.

Profile of the Database

There are 280,721 positions in the database. Here's how they break down according to each position's cubeless probably of winning (CPW).

Cubeless Probability
of Winning		 Number of
Positions		 Fraction of
Positions
0.00 to 0.05
0.05 to 0.10
0.10 to 0.15
0.15 to 0.20
0.20 to 0.25
0.25 to 0.30
0.30 to 0.35
0.35 to 0.40
0.40 to 0.45
0.45 to 0.50
0.50 to 0.55
0.55 to 0.60
0.60 to 0.65
0.65 to 0.70
0.70 to 0.75
0.75 to 0.80
0.80 to 0.85
0.85 to 0.90
0.90 to 0.95
0.95 to 1.00 		86807
9053
6983
6063
5681
5650
5557
5088
5032
4676
4894
4904
5226
5244
5477
5907
6231
7341
9228
85679 		30.9%
3.2%
2.5%
2.2%
2.0%
2.0%
2.0%
1.8%
1.8%
1.7%
1.7%
1.7%
1.9%
1.9%
2.0%
2.1%
2.2%
2.6%
3.3%
30.5%

Unfortunately, many positions in the database have one side or the other as an overwhelming favorite. These are not particularly useful for judging cube handling. But there are still thousands of "good" positions for us to work with.

Equities

All positions in the database were rolled out using the computer program, Gnu Backgammon. Gnu Backgammon is known to be a capable player of noncontact positions, so the results of its rollouts should be accurate. Each position was rolled out four ways:

  • Cubeless. The position is played to conclusion with no doubling cube.
  • Cubeful with a centered cube and assuming the player on-roll does not double the current position (ND).
  • Cubeful with the player on-roll owning a 1-cube and assuming that player does not redouble the current position (NRD).
  • Cubeful with the opponent owning a 2-cube (TAKE).

Many equities were also confirmed by consulting Hugh Sconyers's Bearoff Database.

Equities are recorded from the point of view of the player whose turn it is to roll.

Cube Decisions

The cubeful equities above (ND, NRD, and TAKE) give all the information needed to determine the correct cube action in any position:

  • A position is a correct initial double if TAKE > ND.
  • A position is a correct redouble if TAKE > NRD.
  • A position is a correct take if TAKE < 1.0.
  • A position is a correct pass if TAKE > 1.0.

Here is the number of positions in the database of each type:

Correct initial doubles109,638(39.1%)
Correct redoubles106,777(38.0%)
Correct takes181,227(64.6%)
Correct passes99,494(35.4%)

Obtaining a Copy of the Database

An abridged version of the database (50,000 positions) is available online. You can download it from http://www.bkgm.com/articles/CubeHandlingInRaces/RaceDB.zip. The following diagram shows how the fields are laid out.

 

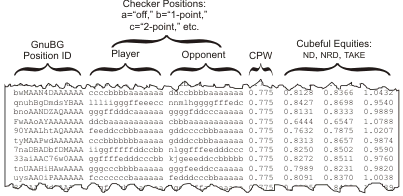
Pip Counting

The single most important measure for determining who is ahead in the race and by how much is the pip count. Your pip count is the total distance your checkers must move to come home and bear off. Or, saying this a different way, your pip count is the minimum total number of pips you must roll to bear off all your checkers.

The importance of the pip count has been recognized just about as long as the doubling cube has been around. Grosvenor Nicholas and Wheaton Vaughan give a method of counting pips in their 1930 book Winning Backgammon: Problems and Answers.

The straightforward method of counting pips is to multiply the number of checkers on each point by the point number, and then add up the products. The following diagram shows the process.

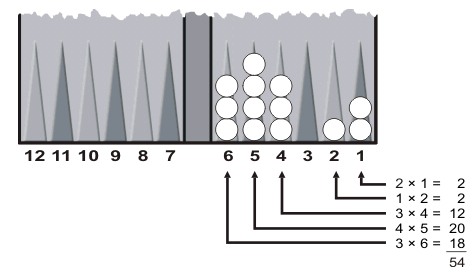
In this example, White's pip count is 54. He will have to roll a minimum of 54 pips (probably more) to bear off all his checkers.

Probability of Winning

If you take your own pip count and compare it to your opponent's pip count, you can get a rough estimate of your chances in the game. The following chart shows your approximate winning chances if it is your turn to roll.

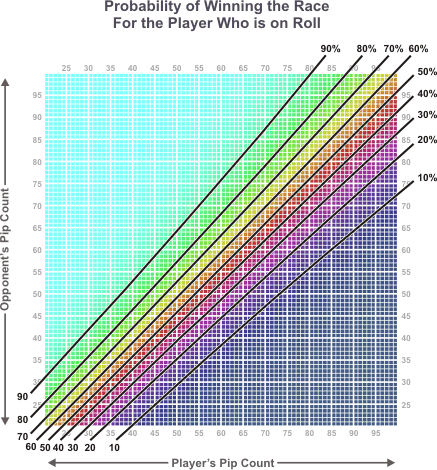
The probabilities in the chart refer to the cubeless probability of winning the game (CPW). They tell you your chance of winning a game if it is played without a doubling cube. When a doubling cube is used, your cubeful equity is more extreme (higher if you are winning, lower if you are losing). Formulas for converting between cubeless and cubeful equities appear later in this article.

Value of a Pip

When the race is even (in terms of pip count), the player whose turn it is can expect to win about 60% of the time. This advantage is because being "on-roll" is equal to about 4 pips, and each extra pip is worth about 2.5% CPW in a close race.

Cubeless Probability
of Winning		 Each Pip
is Worth
10% to 20%about 1.5%
20% to 30%about 2%
30% to 70%about 2.5%
70% to 80%about 2%
80% to 90%about 1.5%
 

Wastage

Unfortunately, the pip count is only part of the story. The other part of the story is wastage. Wastage is the number of pips you expect will go unused when you bear off your final checkers. These pips are lost when you are forced to use a large number to remove a checker from a low-numbered point.

An extreme example of wastage is Red's position below:

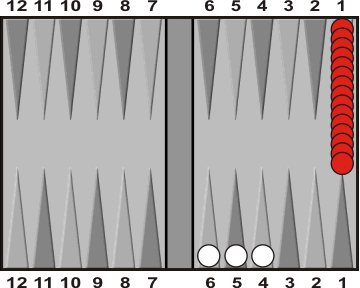
Red has 15 checkers on his one point, giving him a pip count of 15; White has one checker on each of his points 4, 5, and 6, giving him a pip count of 4 + 5 + 6 = 15. Though both players have the same count, it is easy to see that Red will need many more rolls to bear of his checkers than White. That's because Red will waste many pips almost every roll.

Many checkers on low-numbered points lead to wastage.

 
In a different illustration of wastage, look at the following position:

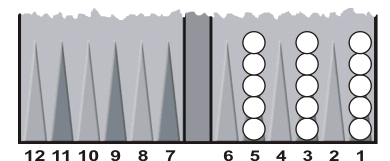
Any time White rolls an even number, he is forced to waste pips. For example, if White rolls a 4, he must move one of his checkers from the five point to the one point. We have already seen that many checkers on a low-numbered point will end up being wasteful. The same type of problem happens if White rolls a 2; he is forced to move a checker onto a point that already has many checkers.

Gaps and high stacks lead to wastage.
 

Advanced Pip Counting Formulas

Is there a way to count pips that takes into consideration wastage?

Over the years many people have proposed formulas that attempt to do that. In this section we will take a look at some of these formulas.

Thorp Count

Perhaps the most famous formula for adjusting the basic pip count was devised by Edward O. Thorp. Thorp is author of the popular Blackjack book, Beat the Dealer, and an expert in the field of probability and gambling theory. The Thorp count works like this:

For each player, start with the basic pip count, then:

  • add 2 pips for each checker that player has on the board;
  • add 1 pip for each checker on the one point;
  • subtract 1 pip for each occupied home-board point.

The resulting adjusted pip count gives a more accurate picture of the relative merits of the players' positions. We will see later how to use the Thorp count to make cube decisions.

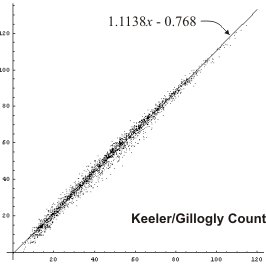
Keeler/Gillogly Count

This counting method was developed by Emmett Keeler and Jim Gillogly. It is essentially the same as the Thorp count except that relative values are used instead of absolute values for the number of checkers still on the board and the number of occupied home-board points.

For each player, start with the basic pip count, then:

  • add 2 pips for each additional checker on the board compared to the opponent;
  • add 1 pip for each checker on the ace-point;
  • subtract 1 pip for each additional home-board point compared to the opponent.

The net effect of Keeler's and Gillogly's alterations to the Thorp formula is to reduce the size of the numbers to be compared. This makes the arithmetic involved a little easier.

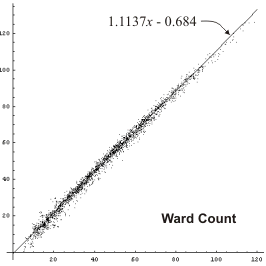
Ward Count

Jeff Ward devised a formula that attempts to improve on the reliability of the Thorp count. His formula works like this:

For each player, start with the basic pip count, then:

  • add 2 pips for each checker more than 2 on the one point;
  • add 1 pip for each checker more than 2 on the two point;
  • subtract 1 pip for each additional home-board point compared to the opponent.
  • add ½ pip for each checker outside the home board;
  • add 2 pips for each additional checker on the board compared to the opponent.

The Ward count is a little harder to use than Thorp or Keeler/Gillogly, but it seems to be more accurate and many experts prefer it.

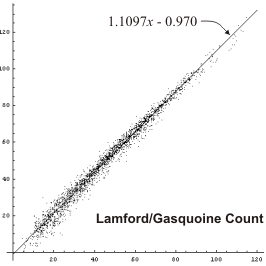
Lamford/Gasquoine Count

Paul Lamford and Simon Gasquoine devised a formula that accounts for wastage primarily by penalizing stacks and gaps. Their formula works like this:

For each player, start with the basic pip count, then:

  • add 2 pips for each additional checker on the board;
  • add 2 pips for each checker more than two on the ace-point;
  • add 1 pip for each checker more than two on the deuce-point;
  • add 1 pip for each checker more than five on any other point, but not if you are also adding a penalty for gaps (see below);
  • add 4 pips for a gap on the four-point;
  • add 3 pips for a gap on the five-point;
  • add 2 pips for a gap on the three-point;
  • add 1 pip for a gap on the two-point;
  • reduce the penalty for a gap by 1 if rolling the number corresponding to the gap allows another gap to be filled.

With so many steps, it's natural to ask: "Is a formula of this length worth learning?" We will see later that Lamford/Gasquoine actually does no better than any of the other counts.

Keith Count

While researching different methods for adjusting pip counts, I thought it would be interesting to see if I could find a way to improve on the other methods. The following formula was developed by trial-and-error using the database of noncontact positions. Here is how it works:

For each player, start with the basic pip count, then

  • add 2 pips for each checker more than 1 on the one point;
  • add 1 pip for each checker more than 1 on the two point;
  • add 1 pip for each checker more than 3 on the three point;
  • add 1 pip for each empty space on points four, five, or six.

We'll see how this formula compares to other counting methods in the next section.  

Comparing the Formulas

How good are these formulas at adjusting for wastage? One way to get a sense of how they compare is to see how good they are at "lining up" positions of equal equity.

Here is an example to illustrate. Let's take a look at all the positions in the database in which the player-on-roll has a CPW of between 74% and 76%. For each such position we'll calculate the pip count of each player, giving an ordered pair (x, y) where x is the player-on-roll's pip count and y is the opponent's pip count. Then we plot the ordered pairs.

The resulting graph looks like this:

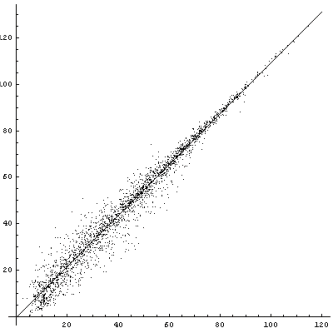
This shows that a straight pip count does only a rough job of lining up points of equal equity.

We can do the same type of plot with the other formulas and see how their graphs compare.

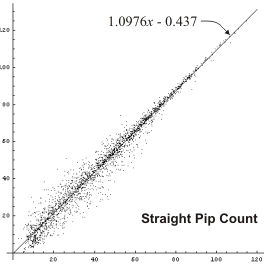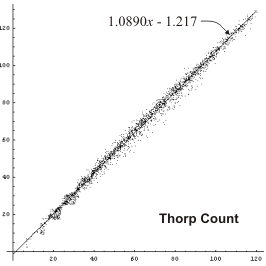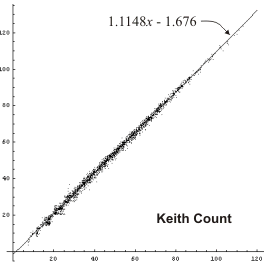We can see that any formula is an improvement over a straight pip count, and the Keith formula seems to do best. Of course this is only a subjective opinion, and we are looking only at positions with CPW around 75%. It would be nice to get some hard numbers, and to compare more positions than just CPW = 75%.

So here is what I did. For each counting method, I found a smooth function of the players' counts that approximated as closely as possible the average CPW of the positions in the database. This gives a way for each counting method to estimate the CPW of a position. Then, for all the positions in the database with a CPW between 50% and 95%, I found the average* error between the CPW estimated by a particular count and the actual CPW.

* Average error was calculated as the square root of the sum of the squares of the differences between the estimated and actual CPW.

The following graph shows the error rate of each method at different length races. The error rate is plotted according to the player-on-roll's pip count.

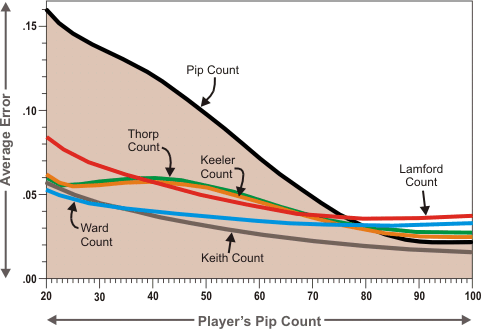
Thorp and Keeler do significantly better than a straight pip count in all but very long races. Lamford does a little better than Thorp in midlength races but not as well at the extremes. Ward count does quite a bit better overall, especially at shorter and midlength races. And Keith count does better than Ward except at very short races.  

Decision Criteria

Now let's look at how to use the various pip formulas for making cube decisions.

A set of decision criteria tells us when to double, when to redouble, when to take, and when to pass. We will use the term double to refer to the first double in a game, and redouble to refer to a subsequent double in the same game. Generally you want to have a slightly stronger position to redouble than to double.

The 8-9-12 Rule

The 8-9-12 rule works with a straight pip count. The player-on-roll subtracts his own pip count from the opponent's count.

  • He should double if the difference is 8% or more of his own count.
  • He should redouble if the difference is 9% or more of his own count.
  • The opponent should take if the difference is 12% or less of the doubler's pip count.

For example, suppose your count is 80 and your opponent's count is 90. The difference is 10 pips. Eight percent of 80 is 6.4 pips, so a 10-pip lead is easily enough to double. Nine percent of 80 is 7.2 pips, so 10 pips is also enough to make a redouble. Twelve percent of 80 is 9.6 pips, but since the opponent trails by 10 pips, he doesn't quite have enough to take if a double is offered.

Thorp's Criteria

Thorp's criteria are designed to be used with the Thorp count. For each side, you compute an adjusted count according to Thorp's formula as described in the previous section. The player-on-roll then adds 10% to his own count.

  • He should double if his count is no more than 2 greater than the opponent's count.
  • He should redouble if his count is no more than 1 greater than the opponent's count.
  • The opponent should take if the opponent's count is no more than 2 greater than doubler's count.

Thorp's decision criteria are also used with the Keeler/Gillogly count and the Ward count.

Lamford's Criteria

Lamford and Gasquoine don't give specific decision criteria for use with their adjusted pip count. Rather, they provide a formula for converting pip counts into CPW:

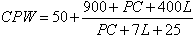
where  CPW =  cubeless probability of winning the game expressed in percent,
 PC  =  pipcount for the player on roll,
 L  =  number of pips lead he has in the race.

You can then use the calculated CPW to make your cube decision. For example, you could say:

  • A player should double if his CPW is greater than 68%.
  • A player should redouble if his CPW is greater than 71%.
  • The opponent should take if the doubler's CPW is less than 78%.

One advantage of this approach is that in match play you have an actual CPW that you can use with a match equity table to adjust your cube decisions according to the score. Of course there is a huge downside—the Lamford/Gasquoine approach is considerably more complicated to apply than any of the other methods presented here.

Keith's Criteria

The following criteria are designed for use with the Keith count. Compute an adjusted count for each side according to the Keith formula. The player-on-roll then increases his own count by one-seventh (rounding down).

  • He should double if his count exceeds the opponent's count by no more than 4.
  • He should redouble if his count exceeds the opponent's count by no more than 3.
  • The opponent should take if doubler's count exceeds the opponent's by at least 2.
 

Comparing Methods

Earlier we saw how the different formulas compared at smoothing out the pip counts to account for wastage. Now let's see how they compare at making cube decisions. To do this, we'll use the database of noncontact positions.

Cubeful Equities

Each position in the database has three cubeful equities:

ND No double. This is the player's cubeful equity if the cube is in the center and he does not double this turn.
NRD No redouble. This is the player's cubeful equity if he owns a 1-cube and does not double this turn.
TAKE   Take. This is the player's cubeful equity if he doubles this turn and his opponent takes.

These equities give all the information we need to make "perfect" cube decisions:

  • A position is a correct double if TAKE > ND.
  • A position is a correct redouble if TAKE > NRD.
  • A position is a correct take if TAKE < 1.0.
  • A position is a correct pass if TAKE > 1.0.

So we can go through the positions in the database and see how often each method makes the correct cube play. And when a method makes an error, we can calculate the size of the error, measured in lost equity.

Chart of Cube Errors

The following chart shows the total errors by each cube-handling method for every position in the database. The three possible types of errors (doubling errors, redoubling errors, and take/pass errors) are shown separately.

Cube Method Doubling Errors Redoubling Errors Take/Pass Errors
8-9-12 Rule 2063.64 2380.06 7493.83
Lamford/Gasquoine 794.13 840.84 1475.70
Thorp 752.82 808.13 2097.53
Keeler/Gillogly 490.17 593.30 1466.11
Ward 435.98 526.23 1202.67
Keith 348.66 353.63 633.89

High numbers in the chart are bad; they indicate either that a particular cubing method makes a lot of errors, or that it makes costly errors, or a combination of the two.

The 8-9-12 rule fairs worst. That's because it is using a straight pip count. Any formula that attempts to account for wastage does significantly better. This just shows how important it is to do some kind of wastage adjustment before using a pip count to make cube decisions.

The Lamford/Gasquoine count does a little better than Thorp. However, we will see that the Thorp count is not yet being shown in its best light.

It is interesting to see how much better Keeler/Gillogly does compared to Thorp considering how similar the formulas are.

The Ward count does a little better than Keeler/Gillogly. And the Keith count does the best overall.

A Note about Thorp's Criteria

In Bill Robertie's description of the Thorp count, he says 10% should be added to the player-on-roll's count only if the count is greater than 30. Jeff Ward makes no mention of this condition in his book. I don't know if it was part of Thorp's original formulation or the condition was added later by somebody else. But let's see what happens when we apply the 30-pip condition to Thorp's count, Keeler/Gillogly's count, and Ward's count.

These are the revised error numbers.

Cube Method Doubling Errors Redoubling Errors Take/Pass Errors
8-9-12 Rule 2063.64 2380.06 7493.83
Lamford/Gasquoine 794.13 840.84 1475.70
Thorp* 574.14 579.54 1712.00
Keeler/Gillogly* 401.24 467.17 1239.32
Ward* 378.29 448.97 1032.81
Keith 348.66 353.63 633.89

* 10% added to player-on-roll's count only when count is greater than 30.

As you can see, the 30-pip condition helps quite a bit with all three formulas that use Thorp's criteria.  

Cubeless and Cubeful Equity

Here is some information on the relationship between cubeless and cubeful equities. This information is not necessary for making accurate cube decisions, but it is useful to understand.

The cubeless equity of a position refers to the likelihood of a player winning the game if it is played to conclusion (without a doubling cube). We have been expressing cubeless equity as CPW (cubeless probability of winning).

Cubeful equity refers to the number of points you expect to win or lose when the doubling cube is in play. This depends not only on the position of the checkers, but also on the value of the doubling cube and who owns it.

From the database of noncontact positions, we can find the average cubeful equities at each possible CPW.

Cubeful Equities with a Centered Cube

Here is a chart showing cubeful equities when the doubling cube is in the middle:

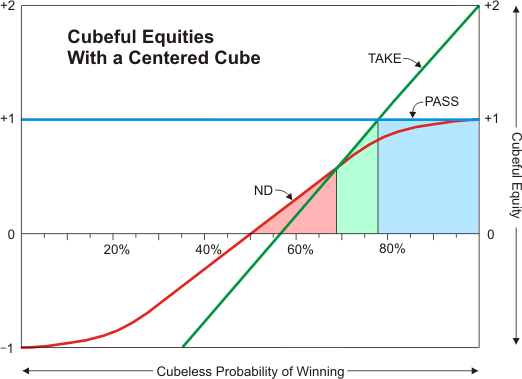
Each colored line represents a different cube action. The red line shows your equity if you don't double. The green line shows your equity if you double and the opponent takes. The blue line shows your equity if you double and the opponent passes.

You can see that when your CPW is less than about 68% the proper cube action is "no double." When your CPW is between about 68% and about 78%, the proper cube action is "double/take." And above 78%, the proper cube action is "double/pass."

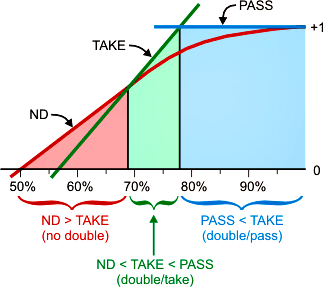
Cubeful Equities When You Own the Cube

Here is a chart showing the cubeful equities when the player-on-roll owns the doubling cube. We are assuming the cube is at 1, even though an owned cube would normally be at 2 or higher.

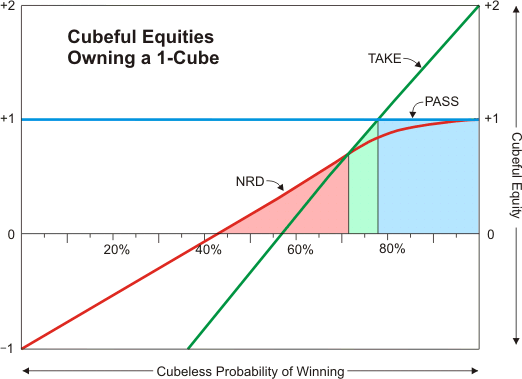
Each colored line represents a different cube action. The red line shows your equity if you don't redouble. The green line shows your equity if you redouble and the opponent takes. The blue line shows your equity if you redouble and the opponent passes.

This looks similar to the centered-cube chart, but there are some important differences. The NRD line has no curve on its left side, so a player has a higher equity before he doubles than in the previous chart. This means you need slightly higher CPW before you can redouble because it takes longer for TAKE to overtake NRD.

When your CPW is less than about 71% the proper cube action is "no redouble." When your CPW is between about 71% and about 78%, the proper cube action is "redouble/take." And above 78%, the proper cube action is "redouble/pass." You can see that the double/take region of this chart is narrower than in the centered-cube chart.

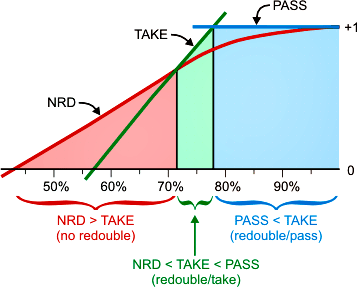
CPW Decision Criteria

Suppose you magically knew your exact cubeless probability of winning the game. What would be your best strategy for handling the cube? The charts above give approximate answers, but can we narrow down the numbers a little more?

I tried varying the decision thresholds and testing them on the positions in the database to see what numbers gave the lowest errors. Here are the results:

  • You should double if your CPW is greater than .682.
  • You should redouble if your CPW is greater than .709.
  • Your opponent should take if your CPW is less than .777.

These are not necessarily the best universal numbers; they are just what worked best on the positions in the database. But the best universal numbers should be close.

Cube Method Doubling Errors Redoubling Errors Take/Pass Errors
CPW 80.31 102.99 18.42

The CPW method of cube handling has a very low error rate compared to the other methods we looked at. Unfortunately, it is usually harder to accurately estimate CPW than it is to make correct cube plays, so this method is really more of academic interest.  

Summary of the Keith Count

For each player, start with the basic pip count and:

  • add 2 pips for each checker more than 1 on the one point;
  • add 1 pip for each checker more than 1 on the two point;
  • add 1 pip for each checker more than 3 on the three point;
  • add 1 pip for each empty space on points four, five, and six.

Increase the count of the player on roll by one-seventh (rounding down).

  • A player should double if his count exceeds the opponent's count by no more than 4.
  • A player should redouble if his count exceeds the opponent's count by no more than 3.
  • The opponent should take if the doubler's count exceeds the opponent's count by at least 2.
 

References

 

July 2004:  Follow-up correspondence archived here.

April 2009:  Stein Kulseth looks at how the length of the race affects the size of the doubling window. See: Keith count doubling window

Page last updated:  June 22, 2011